【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.
参考答案:
【答案】
(1)解:∵BE∥AD,
∴∠E=∠ADE,
∵∠BAD=∠E,
∴∠BAD=∠ADE,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∴∠CAD=∠ADE,
∴ED∥AC;
(2)解:连接AE, 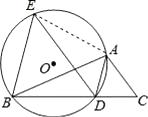
∵∠CAD=∠ADE,∠ADE=∠ABE,
∴∠CAD=∠ABE,
∵∠ADC+∠ADB=180°,∠ADB+∠AEB=180°,
∴∠ADC=∠AEB,
∴△ADC∽△BEA,
∴AC:AB=CD:AE,
∴ABCD=AEAC.
【解析】(1)根据平行线的性质得出∠E=∠ADE,又根据同弧所对的圆周角相等及等量代换得出∠BAD=∠ADE,根据角平分线的定义得出∠BAD=∠CAD,从而得出∠CAD=∠ADE,根据内错角星等二直线平行得出结论;
(2)连接AE,首先根据同弧所对的圆周角相等及等量代换得出∠CAD=∠ABE,然后根据同角的补角相等得出∠ADC=∠AEB,进而判断出△ADC∽△BEA,根据相似三角形对应边成比例得出结论。
【考点精析】本题主要考查了角的平分线和平行线的判定与性质的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC于D,EG⊥BC于G,∠E=∠l,可得AD平分∠BAC,理由如下:
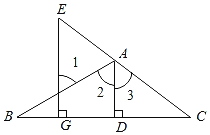
∵AD⊥BC于D,EG⊥BC于G(已知),
∴∠ADC=∠EGC=90° ( ),
∴AD∥EG ( ),
∴∠1= ( ),
∠3=∠E(两直线平行,同位角相等),
又∵∠E=∠1(已知),
∴∠2=∠3 ( ),
∴AD平分∠BAC ( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图1:
竞选人
A
B
C
笔试
85
95
90
口试
80
85

(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图2(没有弃权票,每名学生只能推荐一个),则B在扇形统计图中所占的圆心角是度.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算或方程:
(1)3(x﹣4)3﹣1536=0;
(2)3
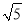 ﹣(
﹣(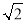 ﹣2
﹣2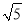 );
);(3)
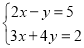 (用代入法);
(用代入法);(4)
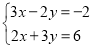 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)23﹣17﹣(﹣7)+(﹣16);
(2)-5+6÷(-2)×
 ;
;(3)-36×
 ;
;(4)﹣23+|5﹣8|+24÷(﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,
 ≈1.7)
≈1.7)
相关试题

