【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ![]() ≈1.7)
≈1.7)
参考答案:
【答案】作CD⊥AB交AB延长线于D, 
设CD=x 米.
Rt△ADC中,∠DAC=25°,
所以tan25°= ![]() =0.5,
=0.5,
所以AD= ![]() =2x.
=2x.
Rt△BDC中,∠DBC=60°,
由tan 60°= ![]() =
= ![]() ,
,
解得:x≈3.
所以生命迹象所在位置C的深度约为3米.
【解析】作CD⊥AB交AB延长线于D,设CD=x 米, 根据正切函数的定义得出AD=2x,再根据特殊锐角的三角函数值及正切定义列出关于x的方程,求解即可得到答案。
【考点精析】关于本题考查的锐角三角函数的定义和特殊角的三角函数值,需要了解锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数;分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.

(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算或方程:
(1)3(x﹣4)3﹣1536=0;
(2)3
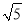 ﹣(
﹣(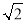 ﹣2
﹣2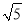 );
);(3)
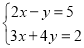 (用代入法);
(用代入法);(4)
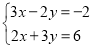 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)23﹣17﹣(﹣7)+(﹣16);
(2)-5+6÷(-2)×
 ;
;(3)-36×
 ;
;(4)﹣23+|5﹣8|+24÷(﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.
计时制:0.05元/分;
包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店计划进A,B两种水果共140千克,这两种水果的进价和售价如表所示
进价
 元
元 千克
千克
售价
 元
元 千克
千克
A种水果
5
8
B种水果
9
13
 若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克? 在
在 的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价
的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价 出售,那么售完后共获利多少元?
出售,那么售完后共获利多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B在数轴上分别表示a、b
(1)对照数轴填写下表:
a
6
-6
-6
-6
-10
-2.5
b
4
0
4
-4
2
-2.5
两点距离
2
6
0
(2)若A、B两点间的距离记为 d,试问d与a、b有何数量关系;
(3)在数轴上找到所有符合条件的整数点P,使它到5和﹣5的距离之和为10,并求出所有这些整数的和;
(4)若数轴上点C表示的数为x,当点C在什么位置时,
①|x+1|的值最小;②|x+1|+|x﹣2|的值最小.
相关试题

