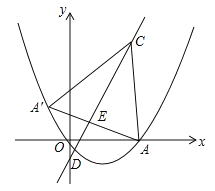
【题目】如图所示,抛物线![]() 经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
(1)求抛物线的解析式,并求出点C和点D的坐标;
(2)求点A关于直线y=2x﹣2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;
(3)点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值.
参考答案:
【答案】(1)![]() ,C(6,10),D(1,0);(2)A′(﹣2,4),A′在抛物线上;(3)l=
,C(6,10),D(1,0);(2)A′(﹣2,4),A′在抛物线上;(3)l=![]() ,(﹣2<x≤6),l的最大值为
,(﹣2<x≤6),l的最大值为![]() .
.
【解析】
试题分析:(1)把点O(0,0),A(6,0)代入![]() ,得:
,得:![]() ,解得:
,解得:![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() .
.
当x=6时,y=2×6﹣2=10,当y=0时,2x﹣2=0,解得x=1,∴点C坐标(6,10),点D的坐标(1,0);
(2)过点A′作AF⊥x轴于点F,∵点D(1,0),A(6,0),可得AD=5,在Rt△ACD中,CD=![]() =
=![]() ,∵点A与点A′关于直线y=2x﹣2对称,∴∠AED=90°,∴S△ADC=
,∵点A与点A′关于直线y=2x﹣2对称,∴∠AED=90°,∴S△ADC=![]() ×
×![]() AE=
AE=![]() ×5×10,解得AE=
×5×10,解得AE=![]() ,∴AA′=2AE=
,∴AA′=2AE=![]() ,DE=
,DE=![]() =
=![]() ,∵∠AED=∠AFA′=90°,∠DAE=∠A′AF,∴△ADE∽△AA′F,∴
,∵∠AED=∠AFA′=90°,∠DAE=∠A′AF,∴△ADE∽△AA′F,∴![]() ,解得AF=4,A′F=8,∴OF=8﹣6=2,∴点A′坐标为(﹣2,4),当x=﹣2时,y=
,解得AF=4,A′F=8,∴OF=8﹣6=2,∴点A′坐标为(﹣2,4),当x=﹣2时,y=![]() ,∴A′在抛物线上.
,∴A′在抛物线上.
(3)∵点P在抛物线上,则点P(x,![]() ),设直线A′C的解析式为y=kx+b,∵直线A经过A′(﹣2,4),C(6,10)两点,∴
),设直线A′C的解析式为y=kx+b,∵直线A经过A′(﹣2,4),C(6,10)两点,∴![]() ,解得:
,解得: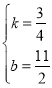 ,∴直线A′C的解析式为
,∴直线A′C的解析式为![]() ,∵点Q在直线A′C上,PQ∥AC,点Q的坐标为(x,
,∵点Q在直线A′C上,PQ∥AC,点Q的坐标为(x,![]() ),∵PQ∥AC,又点Q在点P上方,∴l=(
),∵PQ∥AC,又点Q在点P上方,∴l=(![]() )﹣(
)﹣(![]() )=
)=![]() ,∴l与x的函数关系式为l=
,∴l与x的函数关系式为l=![]() ,(﹣2<x≤6),∵l=
,(﹣2<x≤6),∵l=![]() =
=![]() ,∴当x=
,∴当x=![]() 时,l的最大值为
时,l的最大值为![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学积极组织学生开展课外阅读活动,为了解本校1500名学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

(1)这次抽样调查的样本容量是;
(2)x= , 并将不完整的条形统计图补充完整;
(3)若满足t≥3的人数为合格,那么估计该中学每周课外阅读时间量合格人数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式bx2+2abx+a2b分解因式的结果是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2 , l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;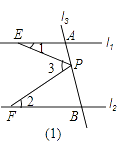
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;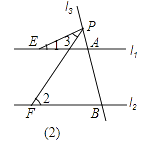
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.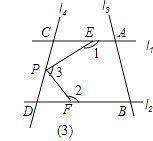
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+x﹣3=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】流花河的警戒水位是33.5米,下表记录的是今年某一周内的水位变化情况,取河流的警戒水位作为0点,并且上周末(星期六)的水位达到警戒水位,(正号表示水位比前一天上升,负号表示水位比前一天下降.)

(1)本周哪一天河流的水位最高?哪一天河流的水位最低?
(2)与上周末相比,本周末河流的水位是上升了还是下降了?
(3)以警戒水位作为零点,用折线统计图表示本周的水位情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3×9m×27m=311 , 则m的值为( )
A.5
B.4
C.3
D.2
相关试题

