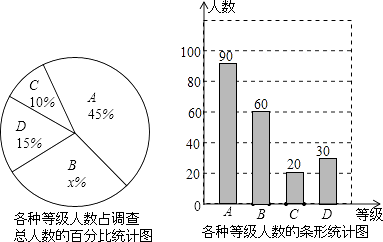
【题目】某中学积极组织学生开展课外阅读活动,为了解本校1500名学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
(1)这次抽样调查的样本容量是;
(2)x= , 并将不完整的条形统计图补充完整;
(3)若满足t≥3的人数为合格,那么估计该中学每周课外阅读时间量合格人数是多少?
参考答案:
【答案】
(1)200
(2)30
(3)解:1500×(10%+15%)=375(人),
则估计中学每周课外阅读时间量合格人数是375人.
【解析】解:(1)根据题意得:90×45%=200(名),
则这次抽样调查的样本容量是200;
所以答案是:200;(2)根据题意得:x%=1﹣(45%+10%+15%)=30%,即x=30,
∵调查的总人数为90÷45%=200(人),
∴B等级人数为200×30%=60(人);
C等级人数为200×10%=20(人),
如图:
(1)由等级A的人数除以占的百分比得到调查总人数即可;
(2)根据扇形统计图求出x的值,根据调查总人数求出等级为B与C的人数,补全条形统计图即可;
(3)根据等级C与D的百分比之和乘以1500即可得到结果.
【考点精析】利用总体、个体、样本、样本容量和扇形统计图对题目进行判断即可得到答案,需要熟知所要考察的全体对象叫总体,组成总体的每一个考察对象叫个体,被抽取的那部分个体组成总体的一个样本,样本中个体的数目叫这个样本的容量(样本容量没有单位);能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某织布厂有 150名工人,为了提高经济效益,增设制衣项目,已知每人每天能织布30m,或利用所织布制衣 4 件,制衣一件需要布 1.5m,将布直接出售,每米布可获利 2 元,将布制成衣后出售,每件可获利 25 元,若每名工人只能做一项工作,且不计其他因素,设安排 x 名工人制衣.
(1)一天中制衣所获利润 元(用含 x 的式表示);
(2)一天中销售剩余的布所获利润为 元(用含 x 的式表示);
(3)一天当中安排 名工人制衣时,所获利润为 13712 元;
(4)一年按 300 天计算,一年中这个工厂所获利润最大值为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】(1.2计算3.4分解因式)
(1)(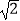 +1)0﹣(﹣
+1)0﹣(﹣  )2+2﹣2
)2+2﹣2
(2)(2a﹣3b)(﹣3b﹣2a)
(3)3m2﹣24m+48
(4)x3y﹣4xy. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:52n=a,4n=b,则102n= ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式bx2+2abx+a2b分解因式的结果是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2 , l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;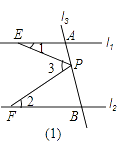
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;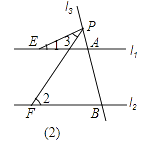
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.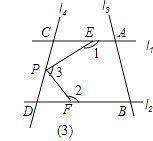
-
科目: 来源: 题型:
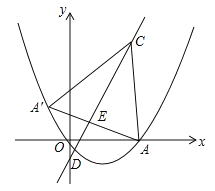
查看答案和解析>>【题目】如图所示,抛物线
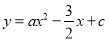 经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.(1)求抛物线的解析式,并求出点C和点D的坐标;
(2)求点A关于直线y=2x﹣2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;
(3)点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值.
相关试题

