【题目】如图,平面直角坐标系中,直线AB:![]() 交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
(1)求直线AB的解析式和点B的坐标;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.

参考答案:
【答案】(1) AB的解析式是y=-![]() x+1.点B(3,0).(2)
x+1.点B(3,0).(2)![]() n-1;(3) (3,4)或(5,2)或(3,2).
n-1;(3) (3,4)或(5,2)或(3,2).
【解析】
试题(1)把A的坐标代入直线AB的解析式,即可求得b的值,然后在解析式中,令y=0,求得x的值,即可求得B的坐标;
(2)过点A作AM⊥PD,垂足为M,求得AM的长,即可求得△BPD和△PAB的面积,二者的和即可求得;
(3)当S△ABP=2时,![]() n-1=2,解得n=2,则∠OBP=45°,然后分A、B、P分别是直角顶点求解.
n-1=2,解得n=2,则∠OBP=45°,然后分A、B、P分别是直角顶点求解.
试题解析:(1)∵y=-![]() x+b经过A(0,1),
x+b经过A(0,1),
∴b=1,
∴直线AB的解析式是y=-![]() x+1.
x+1.
当y=0时,0=-![]() x+1,解得x=3,
x+1,解得x=3,
∴点B(3,0).
(2)过点A作AM⊥PD,垂足为M,则有AM=1,
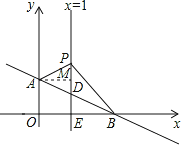
∵x=1时,y=-![]() x+1=
x+1=![]() ,P在点D的上方,
,P在点D的上方,
∴PD=n-![]() ,S△APD=
,S△APD=![]() PDAM=
PDAM=![]() ×1×(n-
×1×(n-![]() )=
)=![]() n-
n-![]()
由点B(3,0),可知点B到直线x=1的距离为2,即△BDP的边PD上的高长为2,
∴S△BPD=![]() PD×2=n-
PD×2=n-![]() ,
,
∴S△PAB=S△APD+S△BPD=![]() n-
n-![]() +n-
+n-![]() =
=![]() n-1;
n-1;
(3)当S△ABP=2时,![]() n-1=2,解得n=2,
n-1=2,解得n=2,
∴点P(1,2).
∵E(1,0),
∴PE=BE=2,
∴∠EPB=∠EBP=45°.
第1种情况,如图1,∠CPB=90°,BP=PC,过点C作CN⊥直线x=1于点N.
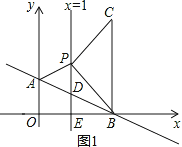
∵∠CPB=90°,∠EPB=45°,
∴∠NPC=∠EPB=45°.
又∵∠CNP=∠PEB=90°,BP=PC,
∴△CNP≌△BEP,
∴PN=NC=EB=PE=2,
∴NE=NP+PE=2+2=4,
∴C(3,4).
第2种情况,如图2∠PBC=90°,BP=BC,
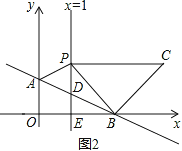
过点C作CF⊥x轴于点F.
∵∠PBC=90°,∠EBP=45°,
∴∠CBF=∠PBE=45°.
又∵∠CFB=∠PEB=90°,BC=BP,
∴△CBF≌△PBE.
∴BF=CF=PE=EB=2,
∴OF=OB+BF=3+2=5,
∴C(5,2).
第3种情况,如图3,∠PCB=90°,CP=EB,
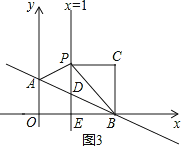
∴∠CPB=∠EBP=45°,
在△PCB和△PEB中,
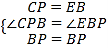
∴△PCB≌△PEB(SAS),
∴PC=CB=PE=EB=2,
∴C(3,2).
∴以PB为边在第一象限作等腰直角三角形BPC,点C的坐标是(3,4)或(5,2)或(3,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某月的月历,用如图恰好能完全遮盖住月历表中的五个数字,设带阴影的“
 ”形中的5个数字的最小数为a.
”形中的5个数字的最小数为a. 请用含a的代数式表示这5个数;
请用含a的代数式表示这5个数; 这五个数的和与“
这五个数的和与“ ”形中心的数有什么关系?
”形中心的数有什么关系? 盖住的5个数字的和能为105吗?为什么?
盖住的5个数字的和能为105吗?为什么?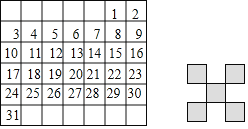
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把
 个边长为1的正方形拼接成一排,求得
个边长为1的正方形拼接成一排,求得  ,
,  ,
,  ,计算
,计算 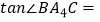 , ……按此规律,写出
, ……按此规律,写出  (用含
(用含  的代数式表示).
的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB>∠ABC.
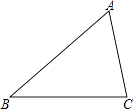
(1)用直尺和圆规在∠ACB的内部作射线CM,使∠ACM=∠ABC(不要求写作法,保留作图痕迹);
(2)若(1)中的射线CM交AB于点D,AB=9,AC=6,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶总D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(结果精确到0.1m。参考数据:tan20°≈0.36,tan18°≈0.32)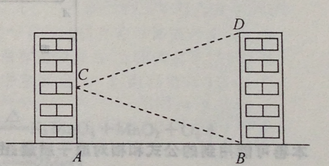
(1)求∠BCD的度数.
(2)求教学楼的高BD -
科目: 来源: 题型:
查看答案和解析>>【题目】金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据:
 ≈1.41,
≈1.41, 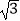 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,点P的坐标为(m+1,m﹣1).
(1)试判断点P是否在一次函数y=x﹣2的图象上,并说明理由;
(2)如图,一次函数y=﹣ x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.
x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.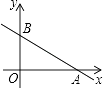
相关试题

