【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 经过点M(1,3)和N(3,5)
经过点M(1,3)和N(3,5)
(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.

参考答案:
【答案】(1)抛物线与x轴没有交点;(2)先向左平移3个单位,再向下平移3个单位或将原抛物线先向左平移2个单位,再向下平移5个单位.
【解析】
试题分析:(1)把M、N两点的坐标代入抛物线解析式可求得a、b的值,可求得抛物线解析式,再根据一元二次方程根的判别式,可判断抛物线与x轴的交点情况;
(2)利用A点坐标和等腰三角形的性质可求得B点坐标,设出平移后的抛物线的解析式,把A、B的坐标代入可求得平移后的抛物线的解析式,比较平移前后抛物线的顶点的变化即可得到平移的过程.
试题解析:
(1)由抛物线过M、N两点,把M、N坐标代入抛物线解析式可得:![]() ,解得:
,解得:![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ,令y=0可得
,令y=0可得![]() ,该方程的判别式为△=9﹣4×1×5=9﹣20=﹣11<0,∴抛物线与x轴没有交点;
,该方程的判别式为△=9﹣4×1×5=9﹣20=﹣11<0,∴抛物线与x轴没有交点;
(2)∵△AOB是等腰直角三角形,A(﹣2,0),点B在y轴上,∴B点坐标为(0,2)或(0,﹣2),可设平移后的抛物线解析式为![]() :
:
①当抛物线过点A(﹣2,0),B(0,2)时,代入可得:![]() ,解得:
,解得:![]() ,∴平移后的抛物线为
,∴平移后的抛物线为![]() ,∴该抛物线的顶点坐标为(
,∴该抛物线的顶点坐标为(![]() ,
,![]() ),而原抛物线顶点坐标为(
),而原抛物线顶点坐标为(![]() ,
,![]() ),∴将原抛物线先向左平移3个单位,再向下平移3个单位即可获得符合条件的抛物线;
),∴将原抛物线先向左平移3个单位,再向下平移3个单位即可获得符合条件的抛物线;
②当抛物线过A(﹣2,0),B(0,﹣2)时,代入可得:![]() ,解得:
,解得:![]() ,∴平移后的抛物线为
,∴平移后的抛物线为![]() ,∴该抛物线的顶点坐标为(
,∴该抛物线的顶点坐标为(![]() ,
,![]() ),而原抛物线顶点坐标为(
),而原抛物线顶点坐标为(![]() ,
,![]() ),∴将原抛物线先向左平移2个单位,再向下平移5个单位即可获得符合条件的抛物线.
),∴将原抛物线先向左平移2个单位,再向下平移5个单位即可获得符合条件的抛物线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 (m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线
(m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线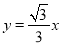 相交于点E,与x轴相交于点D,点P在直线
相交于点E,与x轴相交于点D,点P在直线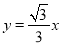 上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.
上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.(1)如图①所示,若抛物线顶点的纵坐标为
 ,求抛物线的解析式;
,求抛物线的解析式;(2)求A、B两点的坐标;
(3)如图②所示,小红在探究点P的位置发现:当点P与点E重合时,∠PDF的大小为定值,进而猜想:对于直线
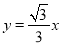 上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.平行四边形的对角线相等
B.一组对边平行,一组对边相等的四边形是平行四边形
C.对角线互相平分的四边形是平行四边形
D.有两对邻角互补的四边形是平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=﹣x2+4的图象的对称轴是( )
A. 直线x=2B. 直线x=﹣2C. y轴D. 直线x=4
-
科目: 来源: 题型:
查看答案和解析>>【题目】用不等式表示“x的2倍与5的差是负数”正确的是( )
A.2x-5>0
B.2x-5<0
C.2x-5≠0
D.2x-5≤0 -
科目: 来源: 题型:
查看答案和解析>>【题目】设x1,x2是一元二次方程x2﹣2x﹣5=0的两根,则x12+x22的值为( )
A. 6B. 8C. 14D. 16
-
科目: 来源: 题型:
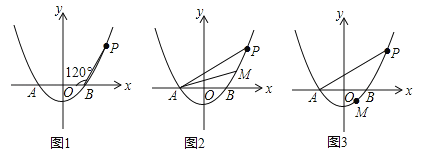
查看答案和解析>>【题目】已知抛物线
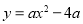 (a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.(1)求抛物线的解析式.
(2)设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为
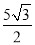 ?若存在,求点M的坐标;若不存在,请说明理由.
?若存在,求点M的坐标;若不存在,请说明理由.②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
相关试题

