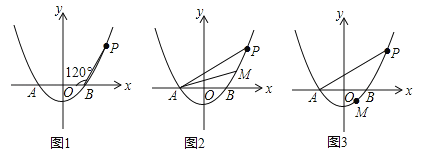
【题目】已知抛物线![]() (a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
(1)求抛物线的解析式.
(2)设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为![]() ?若存在,求点M的坐标;若不存在,请说明理由.
?若存在,求点M的坐标;若不存在,请说明理由.
②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
参考答案:
【答案】(1)![]() ;(2)①存在,M(3,
;(2)①存在,M(3,![]() );②M(
);②M(![]() ,
,![]() )或(
)或(![]() ,
,![]() )时,|m|+|n|的最大值为
)时,|m|+|n|的最大值为![]() .
.
【解析】
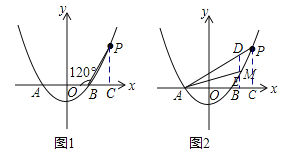
试题分析:(1)先求出A、B两点坐标,然后过点P作PC⊥x轴于点C,根据∠PBA=120°,PB=AB,分别求出BC和PC的长度即可得出点P的坐标,最后将点P的坐标代入二次函数解析式即;
(2)①过点M作ME⊥x轴于点E,交AP于点D,分别用含m的式子表示点D、M的坐标,然后代入△APM的面积公式![]() DMAC,根据题意列出方程求出m的值;
DMAC,根据题意列出方程求出m的值;
②根据题意可知:n<0,然后对m的值进行分类讨论,当﹣2≤m≤0时,|m|=﹣m;当0<m≤2时,|m|=m,列出函数关系式即可求得|m|+|n|的最大值.
试题解析:(1)如图1,令y=0代入![]() ,∴
,∴![]() ,∵a>0,∴
,∵a>0,∴![]() ,∴x=±2,∴A(﹣2,0),B(2,0),∴AB=4,过点P作PC⊥x轴于点C,∴∠PBC=180°﹣∠PBA=60°,∵PB=AB=4,∴cos∠PBC=
,∴x=±2,∴A(﹣2,0),B(2,0),∴AB=4,过点P作PC⊥x轴于点C,∴∠PBC=180°﹣∠PBA=60°,∵PB=AB=4,∴cos∠PBC=![]() ,∴BC=2,由勾股定理可求得:PC=
,∴BC=2,由勾股定理可求得:PC=![]() ,∵OC=OC+BC=4,∴P(4,
,∵OC=OC+BC=4,∴P(4,![]() ),把P(4,
),把P(4,![]() )代入
)代入![]() ,∴
,∴![]() =16a﹣4a,∴a=
=16a﹣4a,∴a=![]() ,∴抛物线解析式为:
,∴抛物线解析式为:![]() ;
;
(2)∵点M在抛物线上,∴![]() ,∴M的坐标为(m,
,∴M的坐标为(m,![]() );
);
①当点M在曲线PB之间(含端点)移动时,∴2≤m≤4,如图2,过点M作ME⊥x轴于点E,交AP于点D,设直线AP的解析式为y=kx+b,把A(﹣2,0)与P(4,![]() )代入y=kx+b,得:
)代入y=kx+b,得: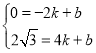 ,解得:
,解得: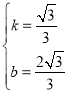 ,∴直线AP的解析式为:
,∴直线AP的解析式为:![]() ,令x=m代入
,令x=m代入![]() ,∴
,∴![]() ,∴D的坐标为(m,
,∴D的坐标为(m,![]() ),∴DM=
),∴DM=![]() =
=![]() ,∴S△APM=
,∴S△APM=![]() DMAE+
DMAE+![]() DMCE
DMCE
=![]() DM(AE+CE)=
DM(AE+CE)=![]() DMAC=
DMAC=![]() ,当S△APM=
,当S△APM=![]() 时,∴
时,∴![]() =
=![]() ,∴解得m=3或m=﹣1,∵2≤m≤4,∴m=3,此时,M的坐标为(3,
,∴解得m=3或m=﹣1,∵2≤m≤4,∴m=3,此时,M的坐标为(3,![]() );
);
②当点M在曲线BA之间(含端点)移动时,∴﹣2≤m≤2,n<0,当﹣2≤m≤0时,∴|m|+|n|=﹣m﹣n=![]() =
=![]() ,当m=
,当m=![]() 时,∴|m|+|n|可取得最大值,最大值为
时,∴|m|+|n|可取得最大值,最大值为![]() ,此时,M的坐标为(
,此时,M的坐标为(![]() ,
,![]() ),当0<m≤2时,∴|m|+|n|=m﹣n=
),当0<m≤2时,∴|m|+|n|=m﹣n=![]() =
=![]() ,当m=
,当m=![]() 时,∴|m|+|n|可取得最大值,最大值为
时,∴|m|+|n|可取得最大值,最大值为![]() ,此时,M的坐标为(
,此时,M的坐标为(![]() ,
,![]() ),综上所述,当点M在曲线BA之间(含端点)移动时,M的坐标为(
),综上所述,当点M在曲线BA之间(含端点)移动时,M的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )时,|m|+|n|的最大值为
)时,|m|+|n|的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线
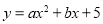 经过点M(1,3)和N(3,5)
经过点M(1,3)和N(3,5)(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用不等式表示“x的2倍与5的差是负数”正确的是( )
A.2x-5>0
B.2x-5<0
C.2x-5≠0
D.2x-5≤0 -
科目: 来源: 题型:
查看答案和解析>>【题目】设x1,x2是一元二次方程x2﹣2x﹣5=0的两根,则x12+x22的值为( )
A. 6B. 8C. 14D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.三角形三条角平分线的交点是三角形的重心
B.三角形的一条角平分线把该三角形分成面积相等的两部分
C.三角形的中线、角平分线、高都是线段
D.三角形的三条高都在三角形内部
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣2,4)关于坐标原点对称的点的坐标为( )
A. (4,﹣2)B. (﹣4,2)C. (2,4)D. (2,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016江西省)设抛物线的解析式为
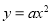 ,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点
,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点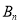 (
(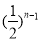 ,0 ) (n为正整数 )作x轴的垂线,交抛物线于点
,0 ) (n为正整数 )作x轴的垂线,交抛物线于点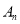 ,连接
,连接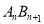 ,得直角三角形
,得直角三角形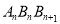 .
.(1)求a的值;
(2)直接写出线段
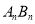 ,
,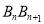 的长(用含n的式子表示);
的长(用含n的式子表示);(3)在系列Rt△
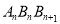 中,探究下列问题:
中,探究下列问题:①当n为何值时,Rt△
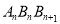 是等腰直角三角形?
是等腰直角三角形?②设1≤k<m≤n (k,m均为正整数),问是否存在Rt△
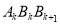 与Rt△
与Rt△ 相似?若存在,求出其相似比;若不存在,说明理由.
相似?若存在,求出其相似比;若不存在,说明理由.
相关试题

