【题目】填空或填写理由.
(1)如图甲,∵∠ =∠ (已知);
∴AB∥CD( )
(2)如图乙,已知直线a∥b,∠3=80°,求∠1,∠2的度数.
解:∵a∥b,( )
∴∠1=∠4( )
又∵∠3=∠4( )
∠3=80°(已知)
∴∠1=( )(等量代换)
又∵∠2+∠3=180°
∴∠2=( )(等式的性质)

参考答案:
【答案】见解析
【解析】
(1)依据内错角相等,两直线平行,即可得到AB∥CD;
(2)依据两直线平行,同位角相等,以及对顶角相等,即可得到∠1,∠2的度数.
(1)如图甲.
∵∠3=∠4(已知);
∴AB∥CD(内错角相等,两直线平行)
故答案为:3,4,内错角相等,两直线平行;
(2)∵a∥b,(已知)
∴∠1=∠4(两直线平行,同位角相等)
又∵∠3=∠4(对顶角相等)
∠3=80°(已知)
∴∠1=∠3=80°(等量代换)
又∵∠2+∠3=180°,
∴∠2=100°(等式的性质)
故答案为:已知,两直线平行,同位角相等,对顶角相等,80°,100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将5个边长为1的正方形按照如图所示方式摆放,O1,O2,O3,O4,O5是正方形对角线的交点,那么阴影部分面积之和等于________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某新建成学校举行美化绿化校园活动,九年级计划购买A,B两种花木共100棵绿化操场,其中A花木每棵50元,B花木每棵100元.
(1)若购进A,B两种花木刚好用去8000元,则购买了A,B两种花木各多少棵?
(2)如果购买B花木的数量不少于A花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.

(1)求证:四边形EDFG是正方形;
(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=k1x+5(k1<0)的图象与坐标轴交于A,B两点,与反比例函数y=
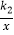 (k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
(k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.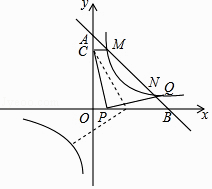
(1)求k2﹣k1的值;
(2)若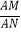 =
=  ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)在(2)的条件下,设点P是x轴(除原点O外)上一点,将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.
B.(a2)3=a6
C.3a?2a=6a
D.3﹣2=﹣6 -
科目: 来源: 题型:
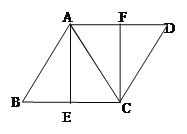
查看答案和解析>>【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF
(1)填空∠B=_______°;
(2)求证:四边形AECF是矩形.
相关试题

