【题目】如图,一次函数y=k1x+5(k1<0)的图象与坐标轴交于A,B两点,与反比例函数y= ![]() (k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
(k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.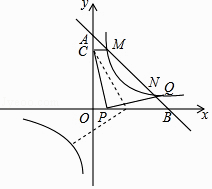
(1)求k2﹣k1的值;
(2)若 ![]() =
= ![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)在(2)的条件下,设点P是x轴(除原点O外)上一点,将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由.
参考答案:
【答案】
(1)
解:∵MC⊥y轴于点C,且CM=1,
∴M的横坐标为1,
当x=1时,y=k1+5,
∴M(1,k1+5),
∵M在反比例函数的图象上,
∴1×(k1+5)=k2,
∴k2﹣k1=5
(2)
解:如图1,过N作ND⊥y轴于D,
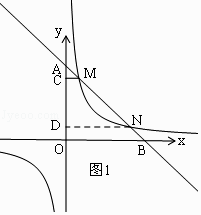
∴CM∥DN,
∴△ACM∽△ADN,
∴ ![]() ,
,
∵CM=1,
∴DN=4,
当x=4时,y=4k1+5,
∴N(4,4k1+5),
∴4(4k1+5)=k2①,
由(1)得:k2﹣k1=5,
∴k1=k2﹣5②,
把②代入①得:4(4k2﹣20+5)=k2,
k2=4;
∴反比例函数的解析式:y= ![]()
(3)
解:当点P滑动时,点Q能在反比例函数的图象上;
如图2,

CP=PQ,∠CPQ=90°,
过Q作QH⊥x轴于H,
易得:△COP≌△PHQ,
∴CO=PH,OP=QH,
由(2)知:反比例函数的解析式:y= ![]() ;
;
当x=1时,y=4,
∴M(1,4),
∴OC=PH=4,
设P(x,0),
∴Q(x+4,x),
当点Q落在反比例函数的图象上时,
x(x+4)=4,
x2+4x+4=8,
x=﹣2± ![]() ,
,
当x=﹣2+2 ![]() 时,x+4=2+2
时,x+4=2+2 ![]() ,如图2,Q(2+2
,如图2,Q(2+2 ![]() ,﹣2+2
,﹣2+2 ![]() );
);

当x=﹣2﹣2 ![]() 时,x+4=2﹣2
时,x+4=2﹣2 ![]() ,如图3,Q(2﹣2
,如图3,Q(2﹣2 ![]() ,﹣2﹣2
,﹣2﹣2 ![]() );
);
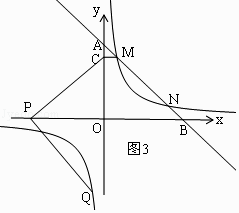
如图4,CP=PQ,∠CPQ=90°,设P(x,0),
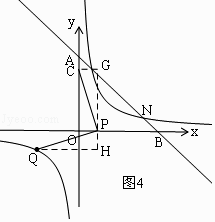
过P作GH∥y轴,过C作CG⊥GH,过Q作QH⊥GH,
易得:△CPG≌△PQH,
∴PG=QH=4,CG=PH=x,
∴Q(x﹣4,﹣x),
同理得:﹣x(x﹣4)=4,
解得:x1=x2=2,
∴Q(﹣2,﹣2),
综上所述,点Q的坐标为(2+2 ![]() ,﹣2+2
,﹣2+2 ![]() )或(2﹣2
)或(2﹣2 ![]() ,﹣2﹣2
,﹣2﹣2 ![]() )或(﹣2,﹣2).
)或(﹣2,﹣2).
【解析】(1)根据点M的坐标代入反比例关系:y= ![]() 中,可得结论;(2)根据△ACM∽△ADN,得
中,可得结论;(2)根据△ACM∽△ADN,得 ![]() ,由CM=1得DN=4,同理得N的坐标,代入反比例函数式中可得k2的值;(3)如图2,点P在x轴的正半轴上时,绕P顺时针旋转到点Q,根据△COP≌△PHQ,得CO=PH,OP=QH,设P(x,0),表示Q(x+4,x),代入反比例函数的关系式中可得Q的两个坐标;
,由CM=1得DN=4,同理得N的坐标,代入反比例函数式中可得k2的值;(3)如图2,点P在x轴的正半轴上时,绕P顺时针旋转到点Q,根据△COP≌△PHQ,得CO=PH,OP=QH,设P(x,0),表示Q(x+4,x),代入反比例函数的关系式中可得Q的两个坐标;
如图3,点P在x轴的负半轴上时;
如图4,点P在x轴的正半轴上时,绕P逆时针旋转到点Q,同理可得结论.
【考点精析】关于本题考查的反比例函数的性质,需要了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某新建成学校举行美化绿化校园活动,九年级计划购买A,B两种花木共100棵绿化操场,其中A花木每棵50元,B花木每棵100元.
(1)若购进A,B两种花木刚好用去8000元,则购买了A,B两种花木各多少棵?
(2)如果购买B花木的数量不少于A花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.

(1)求证:四边形EDFG是正方形;
(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】填空或填写理由.
(1)如图甲,∵∠ =∠ (已知);
∴AB∥CD( )
(2)如图乙,已知直线a∥b,∠3=80°,求∠1,∠2的度数.
解:∵a∥b,( )
∴∠1=∠4( )
又∵∠3=∠4( )
∠3=80°(已知)
∴∠1=( )(等量代换)
又∵∠2+∠3=180°
∴∠2=( )(等式的性质)

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.
B.(a2)3=a6
C.3a?2a=6a
D.3﹣2=﹣6 -
科目: 来源: 题型:
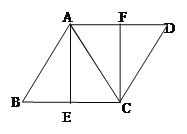
查看答案和解析>>【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF
(1)填空∠B=_______°;
(2)求证:四边形AECF是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是等腰△ABC底边BC上的高,sinB=
 ,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )
,点E在AC上,且AE:EC=2:3,则tan∠ADE=( ) 
A.
B.
C.
D.
相关试题

