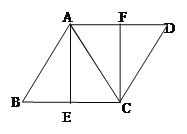
【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF
(1)填空∠B=_______°;
(2)求证:四边形AECF是矩形.
参考答案:
【答案】(1)60;(2)见解析
【解析】(1)根据菱形的性质可得AB=BC,然后根据AB=AC,可得△ABC为等边三角形,继而可得出∠B=60°;
(2)根据△ABC为等边三角形,同理得出△ACD为等边三角形,然后根据E、F分别是BC、AD的中点,可得AE⊥BC,CF⊥AD,然后根据AF∥CE,即可判定四边形AECF为矩形.
(1)(1)因为四边形ABCD为菱形,
∴AB=BC,
∵AC=AB,
∴△ABC为等边三角形,
∴∠B=60°,;
(2)证明:
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∵E.F分别是BC.AD的中点,
∴CE=![]() BC,AF=
BC,AF=![]() AD,
AD,
∴AF=CE,
∴四边形AECF是平行四边形,
∵AB=AC,E是BC的中点,
∴AE⊥BC,即∠AEC=90°,
∴ 四边形AECF是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空或填写理由.
(1)如图甲,∵∠ =∠ (已知);
∴AB∥CD( )
(2)如图乙,已知直线a∥b,∠3=80°,求∠1,∠2的度数.
解:∵a∥b,( )
∴∠1=∠4( )
又∵∠3=∠4( )
∠3=80°(已知)
∴∠1=( )(等量代换)
又∵∠2+∠3=180°
∴∠2=( )(等式的性质)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=k1x+5(k1<0)的图象与坐标轴交于A,B两点,与反比例函数y=
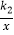 (k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
(k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.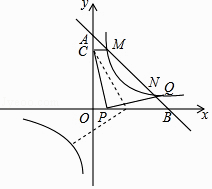
(1)求k2﹣k1的值;
(2)若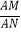 =
=  ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)在(2)的条件下,设点P是x轴(除原点O外)上一点,将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.
B.(a2)3=a6
C.3a?2a=6a
D.3﹣2=﹣6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是等腰△ABC底边BC上的高,sinB=
 ,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )
,点E在AC上,且AE:EC=2:3,则tan∠ADE=( ) 
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
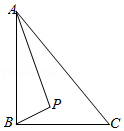
A.
B.2
C.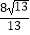
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行“校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出
 名选手组成初中代表队和高中代表队参加学校决赛.每个队
名选手组成初中代表队和高中代表队参加学校决赛.每个队 名选手的决赛成绩如图所示:
名选手的决赛成绩如图所示:
 填表:
填表:平均数(分)
中位数(分)
众数(分)
初中代表队


高中代表队


 结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好; 计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
相关试题

