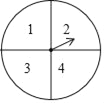
【题目】元旦期间,某商场设置了如图所示的幸运转盘,转盘分成4个大小相同的扇形,分别标有数学1,2,3,4,指针的位置固定,转盘可以自由转动,当转动的转盘停止后,其中的某个扇形会停在指针所指的位置(指针指向两个扇形的交线时,当作右边的扇形).商场规定:凡是参加抽奖的顾客均可转动转盘两次,如果两次转动中指针指缶扇形上的数字之和为8是一等奖,数字之和为7是二等奖,数字之和为6是三等奖,标号之和为其他数字则获得一份纪念品,请分别求出顾客抽中一、二、三等奖的概率.
参考答案:
【答案】![]()
【解析】试题分析:画树状图展示所有16种等可能出现的结果数,再找出转出的两个数字之和为8的结果数、数字之和为7的结果数和数字之和为6的结果数,然后根据概率公式求解.
试题解析:
解:画出树状图为:
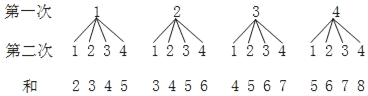
由树状图可以看出,所有可能出现的结果共有16种,并且每种结果出现的可能性都相等.其中转出的两个数字之和为8的结果有1种,数字之和为7的结果有2种,数字之和为6的结果有3种,
所以P(一等奖)=![]() ,P(二等奖)=
,P(二等奖)=![]() =
=![]() ,P(三等奖)=
,P(三等奖)=![]() .
.
-
科目: 来源: 题型:
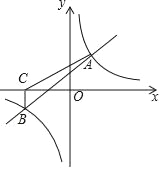
查看答案和解析>>【题目】如图,一次函数y=x+2与反比例函数y=
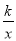 的图象相交于A(2,m),B(﹣4,n)两点.
的图象相交于A(2,m),B(﹣4,n)两点.(1)求反比例函数的解析式;
(2)根据所给条件,请直接写出不等式x+2>
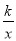 的解集: ;
的解集: ;(3)过点B作BC⊥x轴,垂足为C,连接AC,求S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,∠l=∠2.

(1)求证:∠GFH与∠BHC互补;(2)若∠A=75°,FG⊥AC,求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分钟的速度到达图书馆,而妈妈始终以120米/分钟的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图像,解答下列问题:
(1)图书馆到小燕家的距离是 米;
(2)a= ,b= ,m= ;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是 ;定义域是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,关于
 ,
, 的方程组
的方程组 的解满足
的解满足 ,
, .
.(1)求
 的取值范围;
的取值范围;(2)化简
 ;
;(3)若
 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数图象经过(﹣2,4).
(1)如果点(a,1)和(﹣1,b)在函数图象上,求a,b的值;
(2)过图象上一点P作y轴的垂线,垂足为Q,S△OPQ=
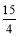 ,求Q的坐标.
,求Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,完成相应学习任务:
四点共圆的条件
我们知道,过任意一个三角形的三个顶点能作一个圆,过任意一个四边形的四个顶点能作一个圆吗?小明经过实践探究发现:过对角互补的四边形的四个顶点能作一个圆,下面是小明运用反证法证明上述命题的过程:
已知:在四边形ABCD中,∠B+∠D=180°.
求证:过点A、B、C、D可作一个圆.
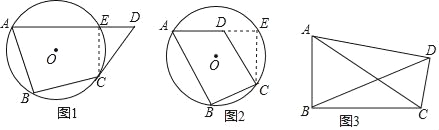
证明:如图(1),假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆外,设AD与圆相交于点E,连接CE,则∠B+∠AEC=180°,而已知∠B+∠D=180°,所以∠AEC=∠D,而∠AEC是△CED的外角,∠AEC>∠D,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
如图(2)假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆内,设AD的延长线与圆相交于点E,连接CE,则∠B+∠AEC=180°,而已知∠B+∠ADC=180°,所以∠AEC=∠ADC,而∠ADC是△CED的外角,∠ADC>∠AEC,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
因此得到四点共圆的条件:过对角互补的四边形的四个顶点能作一个圆.
学习任务:
(1)材料中划线部分结论的依据是 .
(2)证明过程中主要体现了下列哪种数学思想: (填字母代号即可)
A、函数思想 B、方程思想 C、数形结合思想 D、分类讨论思想
(3)如图(3),在四边形ABCD中,∠ABC=∠ADC=90°,∠CAD=16°.AD=BD,则求∠ADB的大小.
相关试题

