【题目】如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,∠l=∠2.

(1)求证:∠GFH与∠BHC互补;(2)若∠A=75°,FG⊥AC,求∠ACB的度数.
参考答案:
【答案】(1)证明见解析;
(2)∠ACB=75°.
【解析】
(1)根据BD平分∠ABC,∠l=∠2,得出FG∥BD,根据平行线的性质得出∠GFH+∠FHD=180°,等量代换即可得到结论;
(2)根据三角形的内角和和角平分线的定义即可得到结论.
(1)证明:∵BD平分∠ABC,
∴∠2=∠ABD,
∵∠1=∠2,
∴∠1=∠ABD,
∴FG∥BD,
∴∠GFH+∠FHD=180°,
∵∠BHC=∠FHD,
∴∠GFH+∠BHC=180°,
∴∠GFH与∠BHC互补;
(2)∵∠A=75°,FG⊥AC,
∴∠1=90°-75°=15°,
∴∠2=∠1=15°,
∵BD平分∠ABC,
∴∠ABC=30°,
∴∠ACB=180°-∠A-∠ABC=75°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠1=65°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为___________.
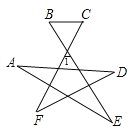
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,点A,B,C,D在一条直线上,填写下列空格:
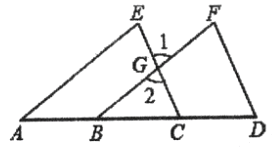
∵AE∥BF(已知)
∴∠E=∠1(______________________)
∵∠E=∠F(已知〉
∴∠_____=∠F(________________)
∴________∥_________(________________________)
-
科目: 来源: 题型:
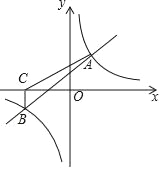
查看答案和解析>>【题目】如图,一次函数y=x+2与反比例函数y=
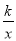 的图象相交于A(2,m),B(﹣4,n)两点.
的图象相交于A(2,m),B(﹣4,n)两点.(1)求反比例函数的解析式;
(2)根据所给条件,请直接写出不等式x+2>
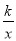 的解集: ;
的解集: ;(3)过点B作BC⊥x轴,垂足为C,连接AC,求S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分钟的速度到达图书馆,而妈妈始终以120米/分钟的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图像,解答下列问题:
(1)图书馆到小燕家的距离是 米;
(2)a= ,b= ,m= ;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是 ;定义域是 .

-
科目: 来源: 题型:
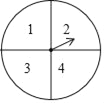
查看答案和解析>>【题目】元旦期间,某商场设置了如图所示的幸运转盘,转盘分成4个大小相同的扇形,分别标有数学1,2,3,4,指针的位置固定,转盘可以自由转动,当转动的转盘停止后,其中的某个扇形会停在指针所指的位置(指针指向两个扇形的交线时,当作右边的扇形).商场规定:凡是参加抽奖的顾客均可转动转盘两次,如果两次转动中指针指缶扇形上的数字之和为8是一等奖,数字之和为7是二等奖,数字之和为6是三等奖,标号之和为其他数字则获得一份纪念品,请分别求出顾客抽中一、二、三等奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,关于
 ,
, 的方程组
的方程组 的解满足
的解满足 ,
, .
.(1)求
 的取值范围;
的取值范围;(2)化简
 ;
;(3)若
 ,求
,求 的取值范围.
的取值范围.
相关试题

