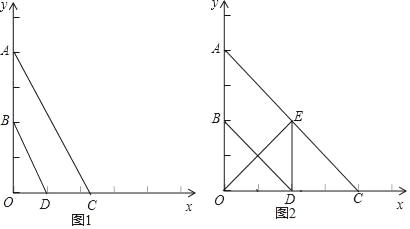
【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
参考答案:
【答案】(1)BD∥AC;(2)点C的坐标为(![]() ,0);(3)直线AC的解析式为y=﹣x+4.
,0);(3)直线AC的解析式为y=﹣x+4.
【解析】试题分析:(1)由A与B的坐标求出OA与OB的长,进而得到B为OA的中点,而D为OC的中点,利用中位线定理即可得证;
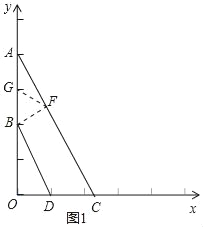
(2)如图1,作BF⊥AC于点F,取AB的中点G,确定出G坐标,由平行线间的距离相等求出BF的长,在直角三角形ABF中,利用斜边上的中线等于斜边的一半求出FG的长,进而确定出三角形BFG为等边三角形,即∠BAC=30°,设OC=x,则有AC=2x,利用勾股定理表示出OA,根据OA的长求出x的值,即可确定出C坐标;
(3)如图2,当四边形ABDE为平行四边形时,AB∥DE,进而得到DE垂直于OC,再由D为OC中点,得到OE=CE,再由OE垂直于AC,得到三角形AOC为等腰直角三角形,求出OC的长,确定出C坐标,设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,即可确定出AC解析式.
试题解析:
(1)∵A(0,4),B(0,2),
∴OA=4,OB=2,点B为线段OA的中点,
又点D为OC的中点,即BD为△AOC的中位线,
∴BD∥AC;
(2)如图1,作BF⊥AC于点F,取AB的中点G,则G(0,3),
∵BD∥AC,BD与AC的距离等于1,
∴BF=1,
∵在Rt△ABF中,∠AFB=90°,AB=2,点G为AB的中点,
∴FG=BG=![]() AB=1,
AB=1,
∴△BFG是等边三角形,∠ABF=60°.
∴∠BAC=30°,
设OC=x,则AC=2x,
根据勾股定理得:OA=![]() ,
,
∵OA=4,
∴x=![]() ,
,
∵点C在x轴的正半轴上,
∴点C的坐标为(![]() ,0);
,0);
(3)如图2,当四边形ABDE为平行四边形时,AB∥DE,
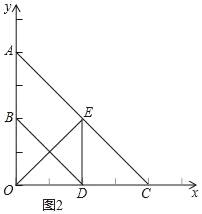
∴DE⊥OC,
∵点D为OC的中点,
∴OE=EC,
∵OE⊥AC,
∴∠OCA=45°,
∴OC=OA=4,
∵点C在x轴的正半轴上,
∴点C的坐标为(4,0),
设直线AC的解析式为y=kx+b(k≠0).
将A(0,4),C(4,0)代入AC的解析式得:
![]()
解得:![]()
∴直线AC的解析式为y=﹣x+4.
-
科目: 来源: 题型:
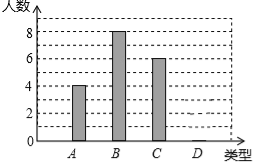
查看答案和解析>>【题目】某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题:
(1)补全条形图;
(2)写出这20名学生每人植树量的众数和中位数;
(3)估计这240名学生共植树多少棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=--
 x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.(1)求AB的长和点C的坐标;
(2)求直线CD的表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
(1)求证:△AEG是等腰直角三角形;
(2)求证:AG+CG=
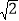 DG.
DG.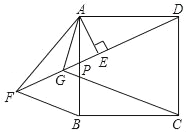
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )

A. 4 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算2a﹣a,正确的结果是( )
A.﹣2a3
B.1
C.2
D.a -
科目: 来源: 题型:
查看答案和解析>>【题目】若a和b都是有理数,则下列①若a≠b,则a2≠b2;②若a>b,则a2>b2;③若a>b,则|a|>|b|;④若a2>b2 , 则a>b说法中,正确的个数是( )
A.0个
B.1个
C.2个
D.3个
相关试题

