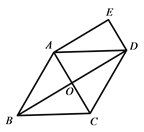
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
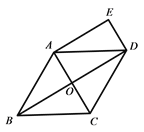
求证:四边形AODE是矩形;(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
参考答案:
【答案】(1)见解析(2)9![]()
【解析】试题分析:
(1)由已知易得四边形AODE是平行四边形,由四边形ABCD是菱形可得AC⊥BD,从而可得∠AOD=90°,由此可得平行四边形AODE是矩形;
(2)由四边形ABCD是菱形,∠BCD=120°易证△ABC是等边三角形,从而可得AC=AB=6,AO=3,结合AC⊥BD由勾股定理可得BO=3![]() ,则OD=3
,则OD=3![]() ,由此可得矩形AODE的面积为
,由此可得矩形AODE的面积为![]() .
.
试题解析:
(1)∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是矩形,
(2)∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=![]() ×4=2,
×4=2,
∵在菱形ABCD中,AC⊥BD,
∴由勾股定理OB=3![]() ,
,
∵四边形ABCD是菱形,
∴OD=OB=3![]() ,
,
∴四边形AODE的面积=OAOD=9![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与
与 相交于点
相交于点 ,
, 是
是 的平分线,
的平分线, ,
, .
.(1)图中除直角外,还有相等的角吗?请写出两对:① ;② .
(2)如果
 ,则①
,则① ;②
;② .
.(3)
 与
与 相等吗? ,理由是 .
相等吗? ,理由是 .(4)如果
 ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
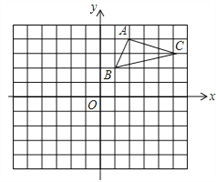
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标A1 ________________.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标A2__________________.
(3) △ABC是否为直角三角形?答_________(填是或者不是).
(4)利用格点图,画出BC边上的高AD,并求出AD的长,AD=_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】6月5日是“世界环境日”,某校从3名男生和2名女生中随机抽取学生去参加市中学生环保演讲比赛.
(1)若抽取1名学生参加,恰好是男生的概率是;
(2)如果抽取1名学生参加,请用列表或树状图求出恰好是1名男生和1名女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=90°,∠BAC=60°,△ABC绕点C顺时针旋转,旋转角为α(0°<α<180°),点A、B的对应点分别是点D、E.
(1)如图1,当点D恰好落在边AB上时,试判断DE与AC的位置关系,并说明理由.
(2)如图2,当点B、D、E三点恰好在一直线上时,旋转角α=__°,此时直线CE与AB的位置关系是__.
(3)在(2)的条件下,联结AE,设△BDC的面积S1,△AEC的面积S2,则S1与S2的数量关系是_____.
(4)如图3,当点B、D、E三点不在一直线上时,(3)中的S1与S2的数量关系仍然成立吗?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从南京到某市可乘坐普通列车,行驶路程是520千米;也可乘坐高铁,行驶路程是400千米.已知高铁的平均速度是普通列车平均速度的2.5倍,且从南京到该市乘坐高铁比乘坐普通列车要少用3小时.求高铁行驶的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

相关试题

