【题目】如图,![]() 为
为![]() 中的一条射线,点
中的一条射线,点![]() 在边
在边![]() 上,
上,![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.

![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 若
若![]() ,试探究
,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
参考答案:
【答案】(1)详见解析;(2)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)根据垂直于同一直线的两直线平行可得PH∥MD,再根据平行于同一直线的两直线平行可得PM∥QR,然后求出四边形PQRM是平行四边形,再求出∠MPQ=90°,根据有一个角是直角的平行四边形是矩形证明即可;
(2)根据矩形的对角线互相平分可得PS=![]() PR,然后求出OP=PS,根据等边对等角的性质可得∠POS=∠PSO,再根据两直线平行,同位角相等可得∠SQR=∠BON,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PSO=2∠SQR,然后整理即可得解.
PR,然后求出OP=PS,根据等边对等角的性质可得∠POS=∠PSO,再根据两直线平行,同位角相等可得∠SQR=∠BON,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PSO=2∠SQR,然后整理即可得解.
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 为矩形;
为矩形;
![]() .理由如下:
.理由如下:
∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,
中, ,线段
,线段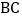 上有动点
上有动点 ,过
,过 作直线
作直线 交
交 边于点
边于点 ,并使得
,并使得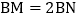 .
. 当
当 与
与 重合时,求
重合时,求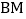 的长;
的长; 在直线
在直线 上是否存在一点
上是否存在一点 ,使得
,使得 是等腰直角三角形?若存在,求出
是等腰直角三角形?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
-
科目: 来源: 题型:
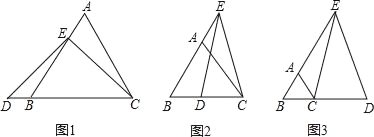
查看答案和解析>>【题目】已知△ABC为等边三角形,E为射线BA上一点,D为直线BC上一点,ED=EC.
(1)当点E在AB的上,点D在CB的延长线上时(如图1),求证:AE+AC=CD;
(2)当点E在BA的延长线上,点D在BC上时(如图2),猜想AE、AC和CD的数量关系,并证明你的猜想;
(3)当点E在BA的延长线上,点D在BC的延长线上时(如图3),请直接写出AE、AC和CD的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形
 ,点
,点 为射线
为射线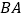 上的一点(不和点
上的一点(不和点 、
、 重合),过
重合),过 作
作 ,且
,且 ,过
,过 作
作 交射线
交射线 于
于 .若
.若 的面积与四边形
的面积与四边形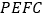 的面积之比为
的面积之比为 ,则
,则 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将
 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转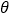 度,并使各边长变为原来的
度,并使各边长变为原来的 倍,得
倍,得 ,即如图①,我们将这种变换记为
,即如图①,我们将这种变换记为 .
. 如图①,对
如图①,对 作变换
作变换 得
得 ,则
,则 ________;直线
________;直线 与直线
与直线 所夹的锐角为________度;
所夹的锐角为________度; 如图②,
如图②, 中,
中, ,
,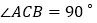 ,对
,对 作变换
作变换 得
得 ,使点
,使点 、
、 、
、 在同一直线上,且四边形
在同一直线上,且四边形 为矩形,求
为矩形,求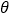 和
和 的值;
的值; 如图③,
如图③,中,  ,
, ,
, ,对
,对 作变换
作变换 得
得 ,使点
,使点 、
、 、
、 在同一直线上,且四边形
在同一直线上,且四边形 为平行四边形,求
为平行四边形,求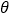 和
和 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)x3x4x5
(2)
 ;
;(3)(﹣2mn2)2﹣4mn3(mn+1);
(4)3a2(a3b2﹣2a)﹣4a(﹣a2b)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.

相关试题

