搜索
【题目】计算
（1）x3x4x5
（2）
；
（3）（﹣2mn2）2﹣4mn3（mn+1）；
（4）3a2（a3b2﹣2a）﹣4a（﹣a2b）2
参考答案：
【答案】（1）x12；（2）﹣12x2y3+2x4y3；（3）﹣4mn3；（4）﹣a5b2﹣6a3．
【解析】
（1）直接用同底数幂的乘法公式计算即可；
（2）用单项式乘以多项式法则进行运算；
（3）先乘方，再乘法，最后合并同类项；
（4）先乘方，再乘法，最后合并同类项．
（1）原式=x3+4+5=x12；
（2）原式=（﹣6xy）×2xy2+（﹣6xy）（﹣
x3y2）=﹣12x2y3+2x4y3；
（3）原式=4m2n4﹣4m2n4﹣4mn3=﹣4mn3；
（4）3a5b2﹣6a3﹣4a×（a4b2）=3a5b2﹣6a3﹣4a5b2=﹣a5b2﹣6a3．
-
科目： 来源： 题型：
查看答案和解析>>【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇，下表是近两周的销售情况：
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
（进价、售价均保持不变，利润=销售收入﹣进货成本）
（1）求A、B两种型号的电风扇的销售单价；
（2）若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A种型号的电风扇最多能采购多少台？
（3）在（2）的条件下，商场销售完这50台电风扇能否实现利润超过1850元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠AOC＝∠BOD＝120°，∠BOC＝
∠AOD．（1）求∠AOD的度数；
（2）若射线OB绕点O以每秒旋转20°的速度顺时针旋转，同时射线OC以每秒旋转15°的速度逆时针旋转，设旋转的时间为t秒（0＜t＜6），试求当∠BOC＝20°时t的值；
（3）若∠AOB绕点O以每秒旋转5°的速度逆时针旋转，同时∠COD绕点O以每秒旋转10°的速度逆时针旋转，设旋转的时间为t秒（0＜t＜18），OM平分∠AOC，ON平分∠BOD，在旋转的过程中，∠MON的度数是否发生改变？若不变，求出其值：若改变，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知线段AD＝80，点B、点C都是线段AD上的点．
（1）如图1，若点M为AB的中点，点N为BD的中点，求线段MN的长；
（2）如图2，若BC＝10，点E是线段AC的中点，点F是线段BD的中点，求EF的长；
（3）如图3，若AB＝5，BC＝10，点P、Q分别从B、C出发向点D运动，运动速度分别为每秒移动1个单位和每秒移动4个单位，运动时间为t秒，点E为AQ的中点，点F为PD的中点，若PE＝QF，求t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线
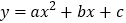过A（2，3），B（4，3），C（6，﹣5）三点．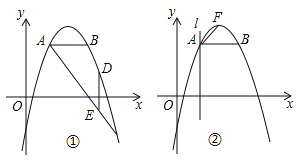
（1）求抛物线的表达式；
（2）如图①，抛物线上一点D在线段AC的上方，DE⊥AB交AC于点E，若满足
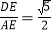，求点D的坐标；（3）如图②，F为抛物线顶点，过A作直线l⊥AB，若点P在直线l上运动，点Q在x轴上运动，是否存在这样的点P、Q，使得以B、P、Q为顶点的三角形与△ABF相似，若存在，求P、Q的坐标，并求此时△BPQ的面积；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；
②方程
的两个根是x1=﹣1，x2=3；③3a+c＞0
④当y＞0时，x的取值范围是﹣1≤x＜3
⑤当x＜0时，y随x增大而增大
其中结论正确的个数是（ ）
A. 4个 B. 3个 C. 2个 D. 1个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
中，
，E为CA延长线上一点，D为AB上一点，F为
外一点且
连接DF，BF.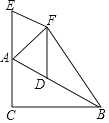
(1)当
的度数是多少时，四边形ADFE为菱形，请说明理由:(2)当AB= 时，四边形ACBF为正方形(请直接写出)
相关试题
