【题目】已知正方形![]() ,点
,点![]() 为射线
为射线![]() 上的一点(不和点
上的一点(不和点![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() ,且
,且![]() ,过
,过![]() 作
作![]() 交射线
交射线![]() 于
于![]() .若
.若![]() 的面积与四边形
的面积与四边形![]() 的面积之比为
的面积之比为![]() ,则
,则![]() ________.
________.

参考答案:
【答案】![]() 或
或![]() .
.
【解析】
作EM⊥BA的延长线于点M,延长EF交BC的延长线于点G,易证△PEM≌△PBC,四边形CDEF为平行四边形,则ME=BP=FG=AB+AP,AP=CG.设AB=BC=1,AP=CG=x,用含x的代数式分别表示S△EFC,S四边形PEFC,根据△EFC与四边形PEFC的面积之比为 3:20,列出关于x的方程,解方程求出x的值,然后根据正切函数的定义即可求出tan∠BPC的值.
作EM⊥BA的延长线于点M,延长EF交BC的延长线于点G,
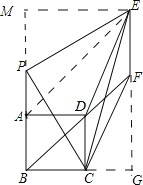
∵PE⊥PC,
∴∠MPE+∠BPC=90°,
∵∠MPE+∠MEP=90°,
∴∠MEP=∠BPC,
在Rt△PBC和Rt△EMP中
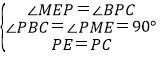
∴Rt△PBC≌Rt△EMP(AAS)
∴PM=BC,ME=PB;
∴PM=AB,
∴PM+PA=AB+PA,
∴MA=ME,
∵MA=ME,AM⊥EM,
∴∠MAE=45°,
∴PB∥EF,
∴四边形ABFE是平行四边形,
∴AB=EF,
∴CD=EF,
∴四边形EFCD是平行四边形,
∴ME=BP=FG=AB+AP,AP=CG,
设AB=BC=1,AP=CG=x,则
S四边形PEFC=S矩形BMEG﹣2S三角形BPC﹣S三角形FCG=(2+x)(1+x)﹣(1+x)﹣![]() (1+x)x=
(1+x)x=![]() x2+
x2+![]() x+1,
x+1,
S△EFC=![]() x;
x;
∵△EFC与四边形PEFC的面积之比为![]() ,
,
∴![]() x:(
x:(![]() x2+
x2+![]() x+1)=3:20,
x+1)=3:20,
解得x=3或![]() ,
,
∵tan∠BPC=![]() ,
,
∴当x=3时,tan∠BPC=![]() ;
;
当x=![]() 时,tan∠BPC=
时,tan∠BPC=![]() .
.
tan∠BPC=![]() 或
或![]() .
.
故答案是:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中, ,
, ,点
,点 从
从 开始沿折线
开始沿折线 以
以 的速度运动,点
的速度运动,点 从
从 开始沿
开始沿 边以
边以 的速度移动,如果点
的速度移动,如果点 、
、 分别从
分别从 、
、 同时出发,当其中一点到达
同时出发,当其中一点到达 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为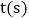 ,当
,当 ________时,四边形
________时,四边形 也为矩形.
也为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,
中, ,线段
,线段 上有动点
上有动点 ,过
,过 作直线
作直线 交
交 边于点
边于点 ,并使得
,并使得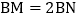 .
. 当
当 与
与 重合时,求
重合时,求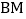 的长;
的长; 在直线
在直线 上是否存在一点
上是否存在一点 ,使得
,使得 是等腰直角三角形?若存在,求出
是等腰直角三角形?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC为等边三角形,E为射线BA上一点,D为直线BC上一点,ED=EC.
(1)当点E在AB的上,点D在CB的延长线上时(如图1),求证:AE+AC=CD;
(2)当点E在BA的延长线上,点D在BC上时(如图2),猜想AE、AC和CD的数量关系,并证明你的猜想;
(3)当点E在BA的延长线上,点D在BC的延长线上时(如图3),请直接写出AE、AC和CD的数量关系.
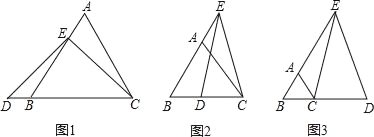
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为
为 中的一条射线,点
中的一条射线,点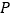 在边
在边 上,
上, 于
于 ,交
,交 于点
于点 ,
, 交
交 于点
于点 ,
,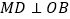 于点
于点 ,
, 交
交 于点
于点 ,连接
,连接 交
交 于点
于点 .
.
 求证:四边形
求证:四边形 为矩形;
为矩形; 若
若 ,试探究
,试探究 与
与 的数量关系,并说明理由.
的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】将
 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转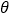 度,并使各边长变为原来的
度,并使各边长变为原来的 倍,得
倍,得 ,即如图①,我们将这种变换记为
,即如图①,我们将这种变换记为 .
. 如图①,对
如图①,对 作变换
作变换 得
得 ,则
,则 ________;直线
________;直线 与直线
与直线 所夹的锐角为________度;
所夹的锐角为________度; 如图②,
如图②, 中,
中, ,
,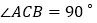 ,对
,对 作变换
作变换 得
得 ,使点
,使点 、
、 、
、 在同一直线上,且四边形
在同一直线上,且四边形 为矩形,求
为矩形,求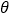 和
和 的值;
的值; 如图③,
如图③,中,  ,
, ,
, ,对
,对 作变换
作变换 得
得 ,使点
,使点 、
、 、
、 在同一直线上,且四边形
在同一直线上,且四边形 为平行四边形,求
为平行四边形,求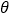 和
和 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)x3x4x5
(2)
 ;
;(3)(﹣2mn2)2﹣4mn3(mn+1);
(4)3a2(a3b2﹣2a)﹣4a(﹣a2b)2
相关试题

