【题目】如图,在长方形![]() 中,
中,![]() ,线段
,线段![]() 上有动点
上有动点![]() ,过
,过![]() 作直线
作直线![]() 交
交![]() 边于点
边于点![]() ,并使得
,并使得![]() .
.
![]() 当
当![]() 与
与![]() 重合时,求
重合时,求![]() 的长;
的长;
![]() 在直线
在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 是等腰直角三角形?若存在,求出
是等腰直角三角形?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

参考答案:
【答案】![]() ;
;![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰直角三角形.
是等腰直角三角形.
【解析】
(1)根据N与A重合时,BN=AB,然后代入数据进行计算即可得解;
(2)分①∠PNM=90°时,求出△APN和△BNM全等,根据全等三角形对应边相等可得AN=BM,AP=BN,然后根据AB=3列出方程计算即可得解;②∠PMN=90°时,过点P作PE⊥BC于E,求出△PME和△MNB全等,根据全等三角形对应边相等可得PE=BM,BN=ME,再根据BE=BM+ME列式计算即可得解;③∠MPN=90°时,过点M作MF⊥AD于F,求出△APN和△FMP全等,根据全等三角形对应边相等可得AP=MF.
![]() 与
与![]() 重合时,
重合时,![]() ,
,
∴![]() ;
;![]() ①
①![]() 时,如图
时,如图![]() ,易得
,易得![]() ,
,
在![]() 和
和![]() 中,
中,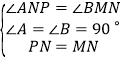 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() ;
;
②![]() 时,如图
时,如图![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,
易得![]() ,
,
在![]() 和
和![]() 中,
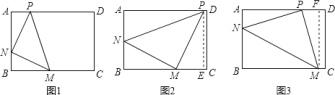
中,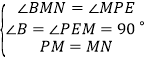 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
③![]() 时,如图
时,如图![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,
易得![]() ,
,
在![]() 和
和![]() 中,
中,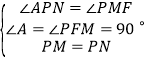 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
综上所述,![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰直角三角形.
是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交BC的延长线于F,若∠F=30°,DE=1,则EF的长是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲村和乙村靠近公路a、b,为了发展经济,甲乙两村准备合建一个工厂,经协商,工厂必须满足以下要求:

(1)到两村的距离相等;
(2)到两条公路的距离相等.你能帮忙确定工厂的位置吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中, ,
, ,点
,点 从
从 开始沿折线
开始沿折线 以
以 的速度运动,点
的速度运动,点 从
从 开始沿
开始沿 边以
边以 的速度移动,如果点
的速度移动,如果点 、
、 分别从
分别从 、
、 同时出发,当其中一点到达
同时出发,当其中一点到达 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为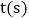 ,当
,当 ________时,四边形
________时,四边形 也为矩形.
也为矩形.
-
科目: 来源: 题型:
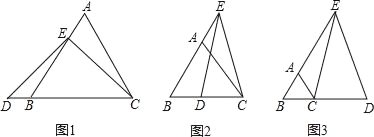
查看答案和解析>>【题目】已知△ABC为等边三角形,E为射线BA上一点,D为直线BC上一点,ED=EC.
(1)当点E在AB的上,点D在CB的延长线上时(如图1),求证:AE+AC=CD;
(2)当点E在BA的延长线上,点D在BC上时(如图2),猜想AE、AC和CD的数量关系,并证明你的猜想;
(3)当点E在BA的延长线上,点D在BC的延长线上时(如图3),请直接写出AE、AC和CD的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形
 ,点
,点 为射线
为射线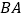 上的一点(不和点
上的一点(不和点 、
、 重合),过
重合),过 作
作 ,且
,且 ,过
,过 作
作 交射线
交射线 于
于 .若
.若 的面积与四边形
的面积与四边形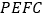 的面积之比为
的面积之比为 ,则
,则 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为
为 中的一条射线,点
中的一条射线,点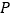 在边
在边 上,
上, 于
于 ,交
,交 于点
于点 ,
, 交
交 于点
于点 ,
,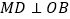 于点
于点 ,
, 交
交 于点
于点 ,连接
,连接 交
交 于点
于点 .
.
 求证:四边形
求证:四边形 为矩形;
为矩形; 若
若 ,试探究
,试探究 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.
相关试题

