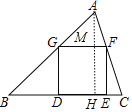
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.

参考答案:
【答案】![]()
【解析】作AH⊥BC于H,交GF于M,如图,先利用三角形面积公式计算出AH=3,设正方形DEFG的边长为x,则GF=x,MH=x,AM=3﹣x,再证明△AGF∽△ABC,则根据相似三角形的性质得![]() ,然后解关于x的方程即可.
,然后解关于x的方程即可.
作AH⊥BC于H,交GF于M,如图,
∵△ABC的面积是6,
∴![]() BCAH=6,
BCAH=6,
∴AH=![]() =3,
=3,
设正方形DEFG的边长为x,则GF=x,MH=x,AM=3﹣x,
∵GF∥BC,
∴△AGF∽△ABC,
∴![]() ,即
,即![]() ,解得x=
,解得x=![]() ,
,
即正方形DEFG的边长为![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为
为 中的一条射线,点
中的一条射线,点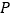 在边
在边 上,
上, 于
于 ,交
,交 于点
于点 ,
, 交
交 于点
于点 ,
,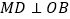 于点
于点 ,
, 交
交 于点
于点 ,连接
,连接 交
交 于点
于点 .
.
 求证:四边形
求证:四边形 为矩形;
为矩形; 若
若 ,试探究
,试探究 与
与 的数量关系,并说明理由.
的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】将
 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转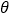 度,并使各边长变为原来的
度,并使各边长变为原来的 倍,得
倍,得 ,即如图①,我们将这种变换记为
,即如图①,我们将这种变换记为 .
. 如图①,对
如图①,对 作变换
作变换 得
得 ,则
,则 ________;直线
________;直线 与直线
与直线 所夹的锐角为________度;
所夹的锐角为________度; 如图②,
如图②, 中,
中, ,
,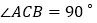 ,对
,对 作变换
作变换 得
得 ,使点
,使点 、
、 、
、 在同一直线上,且四边形
在同一直线上,且四边形 为矩形,求
为矩形,求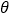 和
和 的值;
的值; 如图③,
如图③,中,  ,
, ,
, ,对
,对 作变换
作变换 得
得 ,使点
,使点 、
、 、
、 在同一直线上,且四边形
在同一直线上,且四边形 为平行四边形,求
为平行四边形,求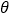 和
和 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)x3x4x5
(2)
 ;
;(3)(﹣2mn2)2﹣4mn3(mn+1);
(4)3a2(a3b2﹣2a)﹣4a(﹣a2b)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=110°,点E、G分别是AB、AC的中点,DE⊥AB交BC于D,FG⊥AC交BC于F,连接AD、AF.试求∠DAF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用 ﹣1来表示
﹣1来表示 的小数部分,事实上,小明的表示方法是有道理的,因为
的小数部分,事实上,小明的表示方法是有道理的,因为 的整数部分是1,将这个数减去其整数部分,差就是
的整数部分是1,将这个数减去其整数部分,差就是 的小数部分,又例如:∵22<(
的小数部分,又例如:∵22<( )2<32,即2<
)2<32,即2< <3,∴
<3,∴ 的整数部分为2,小数部分为(
的整数部分为2,小数部分为( ﹣2).
﹣2).请解答:
(1)
 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .(2)如果
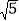 的小数部分为a,
的小数部分为a, 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣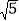 的值.
的值.(3)已知x是3+
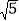 的整数部分,y是其小数部分,直接写出x﹣y的值.
的整数部分,y是其小数部分,直接写出x﹣y的值.
相关试题

