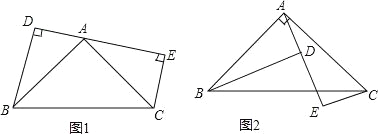
【题目】已知:如图1,△ABC是等腰直角三角形,∠BAC=90°,DE是经过点A的直线,作BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明.
参考答案:
【答案】(1)证明见解析;(2)BD=DE+CE,理由见解析.
【解析】
试题(1)先证△AEC≌△BDA得出AD=CE,BD=AE,从而得出DE=BD+CE;
(2)先证△AEC≌△BDA得出AD=CE,BD=AE,从而得出BD=DE+CE.
试题解析::(1)∵BD⊥DE,CE⊥DE,
∴∠D=∠E=90°,
∴∠DBA+∠DAB=90°,
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠DBA=∠CAE,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∴DE=AD+AE=CE+BD;
(2)BD=DE+CE,理由是:
∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠ABD+∠EAC=90°,
∴∠BAD=∠EAC,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∵AE=AD+DE,
∴BD=CE+DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(a,b)、B(1,4)(a>1)是反比例函数y=
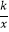 (x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而 . (填“减小”、“不变”或“增大”)
(x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而 . (填“减小”、“不变”或“增大”) 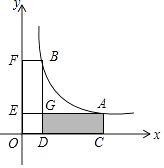
-
科目: 来源: 题型:
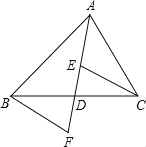
查看答案和解析>>【题目】如图,在△ABC中,点D是BC的中点,连接AD,E,F分别是AD和AD延长线上的点.且DE=DF,连接BF,CE,下列说法中:①△ABD和△ACD的面积相等;②∠BAD=∠CAD;③BF∥CE;④CE=BF,其中,正确的说法有__________(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).
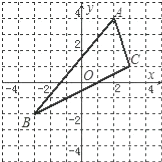
(1)在图中画出△ABC关于y轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标;
(2)求△ABC的面积.
-
科目: 来源: 题型:
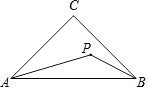
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC=1,P为△ABC内一个动点,∠PAB=∠PBC,则CP的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)解方程组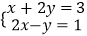
(2)解方程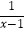 =
= 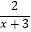 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
相关试题

