【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
参考答案:
【答案】(1)A种机器人每个的进价是2万元,B种机器人每个的进价是4万元;(2)有如下两种方案:方案(1)购买A种机器人的个数是8个,则购买B种机器人的个数是20个;方案(2)购买A种机器人的个数是9个,则购买B种机器人的个数是22个.
【解析】分析:(1)、首先设A种机器人每个的进价是x万元,B种机器人每个的进价是y万元,根据题意列出二元一次方程组,从而得出答案;(2)、设购买A种机器人的个数是m个,则购买B种机器人的个数是(2m+4)个,根据题意列出不等式组,从而求出不等式组的解,根据解为整数得出方案.
详解:解:(1)、设A种机器人每个的进价是x万元,B种机器人每个的进价是y万元,依题意有:![]() , 解得:
, 解得:![]() .
.
故A种机器人每个的进价是2万元,B种机器人每个的进价是4万元;
(2)、设购买A种机器人的个数是m个,则购买B种机器人的个数是(2m+4)个,依题意有
![]() , 解得:8≤m≤9, ∵m是整数, ∴m=8或9,
, 解得:8≤m≤9, ∵m是整数, ∴m=8或9,
故有如下两种方案:
方案(1):m=8,2m+4=20,即购买A种机器人的个数是8个,则购买B种机器人的个数是20个;
方案(2):m=9,2m+4=22,即购买A种机器人的个数是9个,则购买B种机器人的个数是22个.
-
科目: 来源: 题型:
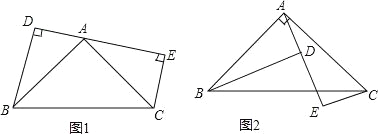
查看答案和解析>>【题目】已知:如图1,△ABC是等腰直角三角形,∠BAC=90°,DE是经过点A的直线,作BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明.
-
科目: 来源: 题型:
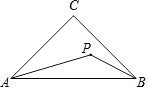
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC=1,P为△ABC内一个动点,∠PAB=∠PBC,则CP的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)解方程组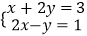
(2)解方程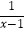 =
= 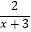 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中,装有2个红球,1个白球,1个黄球,这些球除颜色外都相同.求下列事件的概率:
(1)搅匀后从中任意摸出1个球,恰好是红球;
(2)搅匀后从中任意摸出2个球,2个都是红球. -
科目: 来源: 题型:
查看答案和解析>>【题目】某农产品生产基地收获红薯192吨,准备运给甲、乙两地的承包商进行包销.该基地用大、小两种货车共18辆恰好能一次性运完这批红薯,已知这两种货车的载重量分别为14吨/吨和8吨/辆,运往甲、乙两地的运费如下表:
车型
运费
运往甲地/(元/辆)
运往乙地/(元/辆)
大货车
720
800
小货车
500
650
(1)求这两种货车各用多少辆;
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,总运费为w元,求w关于a的函数关系式;
(2)在(2)的条件下,若甲地的承包商包销的红薯不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在某市五个区投放共享单车供市民使用,投放量的分布及投放后的使用情况统计如下.

(1)该公司在全市一共投放了万辆共享单车;
(2)在扇形统计图中,B区所对应扇形的圆心角为°;
(3)该公司在全市投放的共享单车的使用量占投放量的85%,请计算C区共享单车的使用量并补全条形统计图.
相关试题

