【题目】对任意一个正整数m,如果m=k(k+1),其中k是正整数,则称m为“矩数”,k 为m的最佳拆分点.例如,56=7×(7+1),则56是一个“矩数”,7为56的最佳拆分点.
(1)求证:若“矩数”m是3的倍数,则m一定是6的倍数;
(2)把“矩数”p与“矩数”q的差记为 D(p,q),其中p>q,D(p,q)>0.例如,20=4×5,6=2×3,则 D(20,6)=20﹣6=14.若“矩数”p的最佳拆分点为t,“矩数”q的最佳拆分点为s,当 D(p,q)=30时,求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)证明见解析;(2)最大值是![]() .
.
【解析】试题分析:(1)当k为奇数时,k+1是偶数,则k(k+1)是能被3整除的偶数,故k(k+1)是6的倍数;当k为偶数时,则k(k+1)是能被3整除的偶数,故k(k+1)是6的倍数,
(2)根据题意得p=t(t+1),q=s(s+1),D(p,q)=t(t+1)s(s+1)=30,即![]() 分解因式得到(ts)(t+s+1)=30,根据30=1×30=2×15=3×10=5×6,得到方程组求得
分解因式得到(ts)(t+s+1)=30,根据30=1×30=2×15=3×10=5×6,得到方程组求得![]() 或
或![]() 或
或![]() 或
或![]() 于是得到结论.
于是得到结论.
试题解析:(1)若“矩数”m=k(k+1)是3的倍数,则k(k+1)是3的倍数,k是正整数,
当k为奇数时,k+1是偶数,则k(k+1)是能被3整除的偶数,故k(k+1)是6的倍数;
当k为偶数时,则k(k+1)是能被3整除的偶数,故k(k+1)是6的倍数,
综上所述,若“矩数”m是3的倍数,则m一定是6的倍数;
(2)根据题意得p=t(t+1),q=s(s+1),D(p,q)=t(t+1)s(s+1)=30,
即![]()
∴(ts)(t+s+1)=30,
∵t,s是正整数,t>s,
∴ts,t+s+1是正整数,且t+s+1>ts,
∵30=1×30=2×15=3×10=5×6,
∴![]() 或
或![]() 或
或![]() 或
或![]()
解得: ![]() 或
或![]() 或
或![]() 或
或![]()
∵t,s是正整数,
∴符合条件的是: ![]() 或
或![]() 或
或![]() ,
,
∴![]() 或
或![]() 或
或![]()
∵![]()
∴![]() 的最大值是
的最大值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图案均是由长度相同的火柴按一定的规律拼搭而成,围成的每个小正方形面积为1
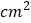 .第一个图案面积为2
.第一个图案面积为2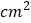 ,第二个图案面积为4
,第二个图案面积为4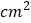 ,第三个图案面积为7
,第三个图案面积为7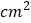 ,…依此规律,第8个图案面积为( )
,…依此规律,第8个图案面积为( )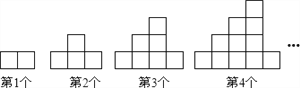
A. 34
 B. 35
B. 35  C. 36
C. 36 D. 37
D. 37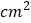
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是轴对称图形,且直线AC是否对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中结论正确的序号是( )

A. ①②③ B. ①②③④ C. ②③④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,过点
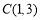 、
、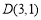 分别作
分别作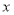 轴的垂线,垂足分别为
轴的垂线,垂足分别为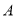 、
、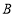 .
.(1)求直线
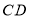 和直线
和直线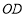 的解析式;
的解析式;(2)点
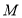 为直线
为直线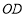 上的一个动点,过
上的一个动点,过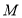 作
作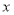 轴的垂线交直线
轴的垂线交直线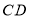 于点
于点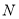 ,是否存在这样的点
,是否存在这样的点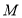 ,使得以
,使得以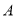 、
、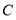 、
、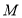 、
、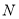 为顶点的四边形为平行四边形?若存在,求此时点
为顶点的四边形为平行四边形?若存在,求此时点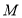 的横坐标;若不存在,请说明理由;
的横坐标;若不存在,请说明理由;(3)若
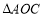 沿
沿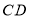 方向平移(点
方向平移(点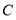 在线段
在线段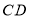 上,且不与点
上,且不与点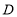 重合),在平移的过程中,设平移距离为
重合),在平移的过程中,设平移距离为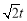 ,
,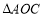 与
与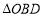 重叠部分的面积记为
重叠部分的面积记为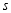 ,试求
,试求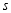 与
与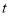 的函数关系式.
的函数关系式.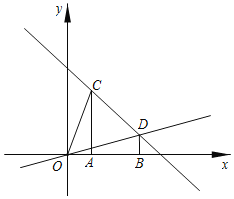
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为12cm,点B,D之间的距离为16m,则线段AB的长为



A.
 B. 10cmC. 20cmD. 12cm
B. 10cmC. 20cmD. 12cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l.若知道l的值,则不需要测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
-
科目: 来源: 题型:
查看答案和解析>>【题目】一快递员需要在规定时间内开车将快递送到某地,若快递员开车每分钟行驶1.2
 ,就早到10分钟;若快递员开车每分钟行驶0.8
,就早到10分钟;若快递员开车每分钟行驶0.8 ,就要迟到5分钟.试求出规定时间及快递员所行驶的总路程.
,就要迟到5分钟.试求出规定时间及快递员所行驶的总路程.小明和小新在解答时先设出未知数,然后列出方程如下:
 ①,
①, ②,其中方程①由小明所列,方程②由小新所列.
②,其中方程①由小明所列,方程②由小新所列.(1)小明所设
 表示 ;
表示 ;小新所设
 表示 .
表示 .(2)请选小明或小新的方法写出完整的解答过程.
相关试题

