搜索
【题目】如图，四边形ABCD是轴对称图形，且直线AC是否对称轴，AB∥CD，则下列结论：①AC⊥BD；②AD∥BC；③四边形ABCD是菱形；④△ABD≌△CDB．其中结论正确的序号是（ ）
A. ①②③ B. ①②③④ C. ②③④ D. ①③④
参考答案：
【答案】B
【解析】
根据轴对称图形的性质，结合菱形的判定方法以及全等三角形的判定方法分析得出答案．
解：如图，因为l是四边形ABCD的对称轴，AB∥CD，
则AD＝AB，∠1＝∠2，∠1＝∠4，
则∠2＝∠4，
∴AD＝DC，
同理可得：AB＝AD＝BC＝DC，
所以四边形ABCD是菱形．
根据菱形的性质，可以得出以下结论：
所以①AC⊥BD，正确；
②AD∥BC，正确；
③四边形ABCD是菱形，正确；
④在△ABD和△CDB中
∵
，
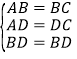∴△ABD≌△CDB（SSS），正确．
故正确的结论是：①②③④．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF等于（）
A.50°B.60°C.70°D.80°
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线
与⊙O，AB是⊙O的直径，AD⊥
于点D．（1）如图①，当直线
与⊙O相切于点C时，若∠DAC=30°，求∠BAC的大小；（2）如图②，当直线
与⊙O相交于点E、F时，若∠DAE=18°，求∠BAF的大小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线
经过点A（3，0），B（﹣1，0）．（1）求抛物线的解析式；
（2）求抛物线的顶点坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】以点A为顶点作等腰Rt△ABC，其中∠BAC=∠DAE=90°，如图1所示放置，使得一直角边重合，连接BD、CE,延长BD交CE于点F.
（1）试判断BD、CE的关系，并说明理由；
（2）把两个等腰直角三角形按如图2所示放置，（1）中的结论是否仍成立？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司销售一种新型节能产品，现准备从国内和国外两种销售方案中选择一种进行销售．若只在国内销售，销售价格y（元/件）与月销量x（件）的函数关系式为y =
x＋150，成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w内（元）（利润=销售额－成本－广告费）．若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a元/件（a为常数，10≤a≤40），当月销量为x（件）时，每月还需缴纳
x2元的附加费，设月利润为w外（元）（利润=销售额－成本－附加费）．（1）当x=1000时，y= 元/件，w内= 元；
（2）分别求出w内，w外与x间的函数关系式（不必写x的取值范围）；
（3）当x为何值时，在国内销售的月利润最大？若在国外销售月利润的最大值与在国内销售月利润的最大值相同，求a的值；
（4）如果某月要将5000件产品全部销售完，请你通过分析帮公司决策，选择在国内还是在国外销售才能使所获月利润较大？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
中，以点
为圆心，
长为半径画弧交
于点
，再分别以点
、为圆心，大于
的相同长为半径画弧，两弧交于点
，连接
并延长交
于点
，连接
，则所得四边形
是菱形．
（1）根据以上尺规作图的过程，求证：四边形
是菱形．（2）若菱形
的周长为16，
，求菱形的面积及
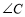的度数．
相关试题
