【题目】将一副直角三角板如图放置,使GM与AB在同一直线上,其中点M在AB的中点处,MN与AC交于点E,∠BAC=30°,若AC=9cm,则EM的长为( )
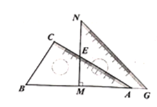
A. 2.5cm B. 3cm C. 4cm D. 4.5cm
参考答案:
【答案】B
【解析】
连接CM,因为点M在AB的中点处,所以由直角三角形斜边上的中线等于斜边的一半可得:CM=AM,△ACM是等腰三角形,再过点M作MF⊥AC于点F,因为∠MEF=60°,可得∠EMF=30°,利用三线合一得出CF=FA=![]() AC=4.5cm,设EM=x,则EF=
AC=4.5cm,设EM=x,则EF=![]() x,EA=EF+FA=
x,EA=EF+FA=![]() x+4.5,
x+4.5,
在Rt△AEM中,因为∠MAE=30°,所以ME=![]() AE,即x=
AE,即x=![]() (
(![]() x+4.5),解得x=3.
x+4.5),解得x=3.
解:连接CM,过点M作MF⊥AC于点F,
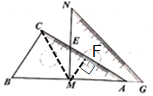
∵点M在AB的中点处,
∴CM=AM=AB,
∵MF⊥AC
∴CF=AF=![]() AC=4.5,
AC=4.5,
∵∠EAM=30°,
∴∠MEA=60° ∠EMF=30°,
设EM=x,则EF=![]() EM=
EM=![]() x,AE=AF+EF=4.5+
x,AE=AF+EF=4.5+![]() x
x
Rt△AME中,∵∠EAM=30°,
∴EM=![]() AE,即x=
AE,即x=![]() (4.5+
(4.5+![]() x),解得x=3,即EM=3.
x),解得x=3,即EM=3.
故答案为:3cm,
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线l1:y=﹣x2+bx+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣
 ).
).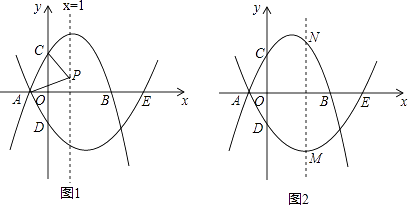
(1)求抛物线l2的函数表达式;
(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标;
(3)M为抛物线l2上一动点,过点M作直线MN∥y轴,交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年6月上海语文把小学教材中“外婆”改成“姥姥一事,引起社会的广泛关注和讨论,明德集团某校文学社就此召开了一次研讨会,为了传承中国传统文化,并组织了一次全体学生“汉字听写”大赛,每位学生听写汉字39个,随机抽取了部分学生的听写结果作为样本进行整理,绘制成如下的统计图表:

组别
正确字数x
人数
A
0≤x<8
10
B
8≤x<16
15
C
16≤x<24
25
D
24≤x<32
m
E
32≤x<40
n
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组“所对应的圆心角的度数是 ;
(3)已知该校共有600名学生,如果听写正确的字的个数不少于24个定为合格,请你估计该校本次听写比赛合格的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明:两直线平行,同旁内角互补(填空).
已知:如图,l1∥l2,l1,l2都被l3所截.
求证:∠1+∠2=180°.
证明:假设∠1+∠2________180°. ∵l1∥l2,∴∠1________∠3. ∵∠1+∠2 _______180°,∴∠3+∠2≠180°,这和________矛盾,∴假设∠1+∠2__________180°不成立,即∠1+∠2=180°.
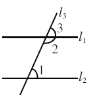
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:在直角三角形中至少有一个角不大于45°.
已知:如图所示,△ABC中,∠C=90°,求证:∠A,∠B中至少有一个不大于45°.
证明:假设__________,则∠A__________45°,∠B______45°. ∴∠A+∠B+∠C>45°+ _______+__________,这与________________________相矛盾. 所以___________不能成立,所以∠A,∠B中至少有一个角不大于45°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,组成这个几何体的小正方体的个数最少是( )
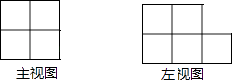
A.5个
B.6个
C.7个
D.8个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC。若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
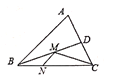
A. 2 B. 4 C. 6 D. 8
相关试题

