【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2 , 请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
参考答案:
【答案】
(1)证明:①当k=0时,方程为x+2=0,所以x=﹣2,方程有实数根,
②当k≠0时,∵△=(2k+1)2﹣4k×2=(2k﹣1)2≥0,即△≥0,
∴无论k取任何实数时,方程总有实数根;
(2)解:令y=0,则kx2+(2k+1)x+2=0,
解关于x的一元二次方程,得x1=﹣2,x2=﹣ ![]() ,
,
∵二次函数的图象与x轴两个交点的横坐标均为整数,且k为正整数,
∴k=1.
∴该抛物线解析式为y=x2+3x+2,
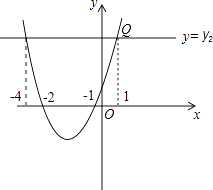
由图象得到:当y1>y2时,a>1或a<﹣4.
(3)解:依题意得kx2+(2k+1)x+2﹣y=0恒成立,即k(x2+2x)+x﹣y+2=0恒成立,
则 ![]() ,
,
解得 ![]() 或
或 ![]() .
.
所以该抛物线恒过定点(0,2)、(﹣2,0).
【解析】(1)分情况讨论:①该方程是一元一次方程时,②该方程是一元二次方程时;(2)通过解kx2+(2k+1)x+2=0得到k=1,由此得到该抛物线解析式为y=x2+3x+2,结合图象回答问题即可;(3)根据题意kx2+(2k+1)x+2﹣y=0恒成立,由此列出关于x、y的方程组,通过解方程组求得该定点坐标.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根,以及对抛物线与坐标轴的交点的理解,了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程2x2+kx﹣1=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是﹣1,求另一个根及k值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OC是∠AOB的平分线,OD是∠AOC的平分线,OE是∠BOD的平分线,且∠BOE=30°,求∠AOB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.

(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为5,sinA= ,求BH的长.
,求BH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B,C,D三点在同一直线上.
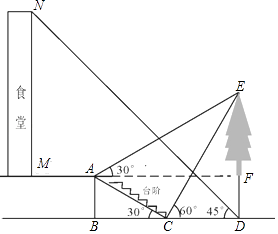
(1)求树DE的高度;
(2)求食堂MN的高度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BF是⊙O的直径,A为⊙O上(异于B、F)一点,⊙O的切线MA与FB的延长线交于点M;P为AM上一点,PB的延长线交⊙O于点C,D为BC上一点且PA=PD,AD的延长线交⊙O于点E.
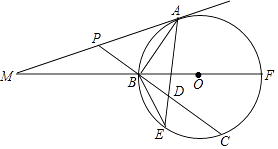
(1)求证: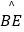 =
= 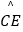 ;
;
(2)若ED、EA的长是一元二次方程x2﹣5x+5=0的两根,求BE的长;
(3)若MA=6 ,sin∠AMF=
,sin∠AMF=  ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】母亲节,是一个感谢母亲的节日,这个节日最早出现在古希腊;而现代的母亲节起源于美国,我国将母亲节定于每年5月的第二个星期日.今年为了在全校进行感恩母亲的宣传,某班通过问卷调查的形式,对2018年5月13日“母亲节”期间,本班全体学生对母亲表达感恩的方式进行调查统计,结果绘制如图:

(1)这个班级共有多少名学生?
(2)扇形统计图中,“帮母亲做家务”所在扇形的圆心角的度数是多少?
(3)补全条形统计图;
(4)若该校有学生1500人,估计该校有多少名学生通过“给母亲一个爱的拥抱”来表达感恩.
相关试题

