【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为5,sinA= ![]() ,求BH的长.
,求BH的长.
参考答案:
【答案】
(1)证明:∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线.
(2)证明:连接AC,如图1所示:
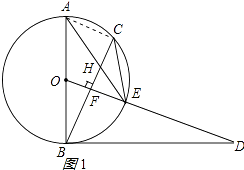
∵OF⊥BC,
∴ ![]() ,
,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴ ![]() ,
,
∴CE2=EHEA;
(3)解:连接BE,如图2所示:
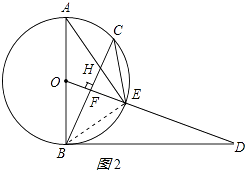
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为5,sin∠BAE= ![]() ,
,
∴AB=10,BE=ABsin∠BAE=10× ![]() =6,
=6,
∴EA= ![]() =
= ![]() =8,
=8,
∵ ![]() ,
,
∴BE=CE=6,
∵CE2=EHEA,
∴EH= ![]() =
= ![]() ,
,
在Rt△BEH中,BH= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由圆周角定理和已知条件,证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;(2)连接AC,由垂径定理得出弧BE=弧CE,得出∠CAE=∠ECB,进而证明出△CEH∽△AEC,得出对应边成比例,即可得出结论;(3)连接BE,由圆周角定理得出∠AEB=90°,由三角函数求出BE的长,再根据勾股定理求出EA,得出BE=CE=6,由(2)的结论求出EH,最后根据勾股定理求出BH即可.
-
科目: 来源: 题型:
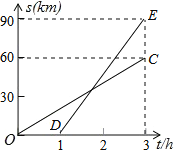
查看答案和解析>>【题目】已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程2x2+kx﹣1=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是﹣1,求另一个根及k值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OC是∠AOB的平分线,OD是∠AOC的平分线,OE是∠BOD的平分线,且∠BOE=30°,求∠AOB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2 , 请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B,C,D三点在同一直线上.
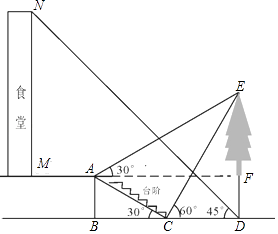
(1)求树DE的高度;
(2)求食堂MN的高度. -
科目: 来源: 题型:
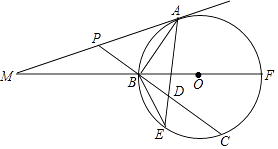
查看答案和解析>>【题目】如图,已知BF是⊙O的直径,A为⊙O上(异于B、F)一点,⊙O的切线MA与FB的延长线交于点M;P为AM上一点,PB的延长线交⊙O于点C,D为BC上一点且PA=PD,AD的延长线交⊙O于点E.
(1)求证: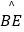 =
= 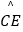 ;
;
(2)若ED、EA的长是一元二次方程x2﹣5x+5=0的两根,求BE的长;
(3)若MA=6 ,sin∠AMF=
,sin∠AMF=  ,求AB的长.
,求AB的长.
相关试题

