【题目】如图,OC是∠AOB的平分线,OD是∠AOC的平分线,OE是∠BOD的平分线,且∠BOE=30°,求∠AOB的度数.

参考答案:
【答案】∠AOB=80°.
【解析】
根据角平分线的定义得到∠BOC=2∠BOE=60°,再根据角平分线的定义得到∠AOB=2∠AOC=2∠BOC=4∠AOD=4∠COD,进一步得到∠BOD=![]() ∠AOB,依此可求∠AOB的度数.
∠AOB,依此可求∠AOB的度数.
因为OE是∠BOD的平分线,∠BOE=30°,
所以∠BOC=2∠BOE=60°,
又因为OC是∠AOB的平分线,OD是∠AOC的平分线,
所以∠AOB=2∠AOC=2∠BOC=4∠AOD=4∠COD,
所以∠BOD=∠BOC+∠COD=3∠COD=3×![]() ∠AOB=
∠AOB=![]() ∠AOB,
∠AOB,
所以∠AOB=![]() ∠BOD=
∠BOD=![]() ×60°=80°,即∠AOB=80°.
×60°=80°,即∠AOB=80°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,OB、OC、OM、ON是
,OB、OC、OM、ON是 内的射线.
内的射线. 如图1,若OM平分
如图1,若OM平分 ,ON平分
,ON平分 当OB绕点O在
当OB绕点O在 内旋转时,则
内旋转时,则 的大小为______;
的大小为______; 如图2,若
如图2,若 ,OM平分
,OM平分 ,ON平分
,ON平分 当
当 绕点O在
绕点O在 内旋转时,求
内旋转时,求 的大小;
的大小; 在
在 的条件下,若
的条件下,若 ,当
,当 在
在 内绕着点O以
内绕着点O以 秒的速度逆时针旋转t秒时,
秒的速度逆时针旋转t秒时, 和
和 中的一个角的度数恰好是另一个角的度数的两倍,求t的值
中的一个角的度数恰好是另一个角的度数的两倍,求t的值
-
科目: 来源: 题型:
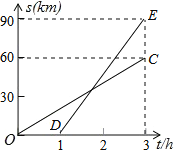
查看答案和解析>>【题目】已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程2x2+kx﹣1=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是﹣1,求另一个根及k值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.

(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为5,sinA= ,求BH的长.
,求BH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2 , 请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B,C,D三点在同一直线上.
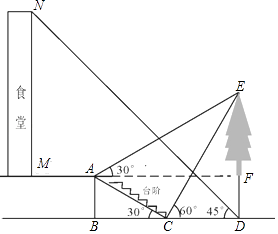
(1)求树DE的高度;
(2)求食堂MN的高度.
相关试题

