【题目】如图,在矩形ABCD中,AB=2,BC=4,P为边AD上一动点,连接BP,把△ABP沿BP折叠,使A落在A′处,当△A′DC为等腰三角形时,AP的长为( )

A. 2B. ![]() C. 2或
C. 2或![]() D. 2或
D. 2或![]()
参考答案:
【答案】C
【解析】
根据△A′DC为等腰三角形,分三种情况进行讨论:①A'D=A'C,②A'D=DC,③CA'=CD,分别求得AP的长,并判断是否符合题意.
①如图,当A′D=A′C时,过A′作EF⊥AD,交DC于E,交AB于F,则EF垂直平分CD,EF垂直平分AB

∴A'A=A'B
由折叠得,AB=A'B,∠ABP=∠A'BP
∴△ABA'是等边三角形
∴∠ABP=30°
∴AP=![]() ;
;
②如图,当A'D=DC时,A'D=2

由折叠得,A'B=AB=2
∴A'B+A'D=2+2=4
连接BD,则Rt△ABD中,BD=![]()
∴A'B+A'D<BD(不合题意)
故这种情况不存在;
③如图,当CD=CA'时,CA'=2

由折叠得,A'B=AB=2
∴A'B+A'C=2+2=4
∴点A'落在BC上的中点处
此时,∠ABP=![]() ∠ABA'=45°
∠ABA'=45°
∴AP=AB=2.
综上所述,当△A′DC为等腰三角形时,AP的长为![]() 或2.
或2.
故选C.
-
科目: 来源: 题型:
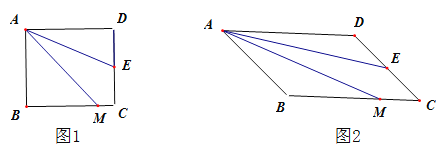
查看答案和解析>>【题目】如图,四边形ABCD是矩形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)证明:AM=AD+MC.
(2)若四边形ABCD是平行四边形,其它条件不变,如图,(1)中的结论是否成立?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在完成第10章的学习后,遇到了一些问题,请你帮助他.
(1)图1中,当
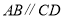 ,试说明
,试说明 .
.(2)图2中,若
 ,则
,则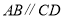 吗?请说明理由.
吗?请说明理由.(3)图3中,
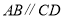 ,若
,若 ,
, ,
, ,
, ,则
,则 ______(直接写出结果,用含x,y,z的式子表示)
______(直接写出结果,用含x,y,z的式子表示)
-
科目: 来源: 题型:
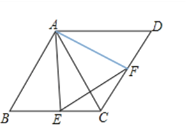
查看答案和解析>>【题目】菱形ABCD中,∠B=60°,点E,F分别是BC,CD上的两个动点,且始终保持∠AEF=60°.
(1)试判断△AEF的形状并说明理由;
(2)若菱形的边长为2,求△ECF周长的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为_________.

-
科目: 来源: 题型:
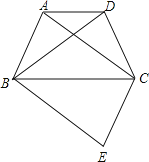
查看答案和解析>>【题目】如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
(1)求证:四边形ABEC是平行四边形.
(2)若AD=CD=6,∠ADC=120°,求四边形ABEC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4交x轴于点A(﹣2,0)和B(B在A右侧),交y轴于点C,直线y=
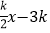 经过点B,交y轴于点D,且D为OC中点.
经过点B,交y轴于点D,且D为OC中点.(1)求抛物线的解析式;
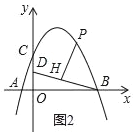
(2)若P是第一象限抛物线上的一点,过P点作PH⊥BD于H,设P点的横坐标是t,线段PH的长度是d,求d与t的函数关系式;
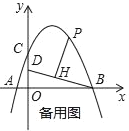
(3)在(2)的条件下,当d=
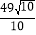 时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.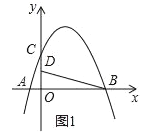
相关试题

