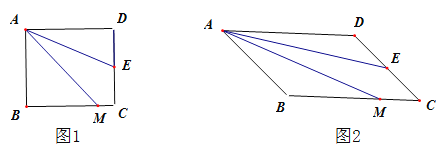
【题目】如图,四边形ABCD是矩形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)证明:AM=AD+MC.
(2)若四边形ABCD是平行四边形,其它条件不变,如图,(1)中的结论是否成立?
参考答案:
【答案】(1)见解析;(2)详见解析.
【解析】
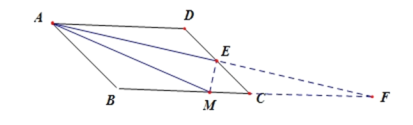
(1)从平行线和中点这两个条件出发,延长AE、BC交于点F,易证Rt△ADE≌Rt△FCE,从而有AD=CF,只需证明AM=MF即可;(2) AM=AD+MC仍然成立,理由为:由四边形ABCD为平行四边形,得到AD与BC平行,利用两直线平行内错角相等得到∠DAE=∠F,再由AE为角平分线得到一对角相等,利用等角对等边得到AM=MF,利用AAS得到三角形ADE与三角形FCE全等,利用全等三角形的对应边相等得到AD=CF,根据AM=MF=AD+MC,即可得证.
(1)延长AE交BC的延长线于点F,

∵E是CD边的中点,
∴DE=EC
∵四边形ABCD是矩形
∴AD//CF
∴∠DAE=∠CFE
又∵AE平分∠DAM
∴∠MAE=∠DAE=∠F
∴AM=MF,
∵∠AED=∠FEC,
∴△ADE≌△FCE(AAS)
∴AD=CF
∴AM=MF=AD+MC;
(2)AM=AD+MC成立,
理由:在平行四边形ABCD中,
∵AD∥BC,
∴∠DAE=∠F,
∵AE平分AE平分∠DAM,
∴∠DAE=∠FAM,
∴∠F=∠FAM,
∴AM=FM,
∵E是CD的中点,
∴DE=CE,
在△ADE和△FCE中,
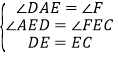 ,
,
∴△ADE≌△FCE(AAS),
∴AD=CF,
∵AM=FM=FC+CM,
∴AM=AD+MC.
-
科目: 来源: 题型:
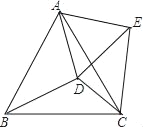
查看答案和解析>>【题目】如图,在等边△ABC 内有一点D,AD=5,BD=6,CD=4,将线段AD绕点A旋转到AE,使∠DAE=∠BAC,连接EC.
(1)求CE的长;
(2)求cos∠CDE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具经销商用32000元购进了一批玩具,上市后恰好全部售完;该经销商又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该经销商第二次购进这种玩具多少套?
(2)由于第二批玩具进价上涨,经销商按第一批玩具售价销售200套后,准备调整售价,发现若每套涨价1元,则会少卖5套,已知第一批玩具售价为200元.设第二批玩具销售200套后每套涨价a元,第二批卖出的玩具总利润w元,问当a取多少时,才能使售出的玩具利润w最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC和△CDE是以C为公共顶点的两个三角形.
(1)如图1,当△ABC和△CDE都是等边三角形时,连接BD、AE相交于点P.求∠DPE的度数;
(2)如图2,当△ABC和△CDE都是等腰直角三角形,且∠ACB=∠DCE=90°时,连接AD、BE,Q为AD中点,连接QC并延长交BE于K.求证:QK⊥BE;
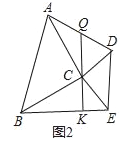
(3)在(1)的条件下,N是线段AE与CD的交点,PF是∠DPE的平分线,与DC交于点F,CN=2
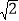 ,∠PFN=45°,求FN的长.
,∠PFN=45°,求FN的长.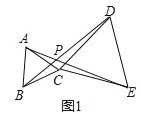
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在完成第10章的学习后,遇到了一些问题,请你帮助他.
(1)图1中,当
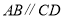 ,试说明
,试说明 .
.(2)图2中,若
 ,则
,则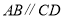 吗?请说明理由.
吗?请说明理由.(3)图3中,
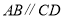 ,若
,若 ,
, ,
, ,
, ,则
,则 ______(直接写出结果,用含x,y,z的式子表示)
______(直接写出结果,用含x,y,z的式子表示)
-
科目: 来源: 题型:
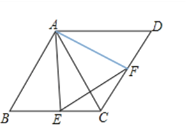
查看答案和解析>>【题目】菱形ABCD中,∠B=60°,点E,F分别是BC,CD上的两个动点,且始终保持∠AEF=60°.
(1)试判断△AEF的形状并说明理由;
(2)若菱形的边长为2,求△ECF周长的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,BC=4,P为边AD上一动点,连接BP,把△ABP沿BP折叠,使A落在A′处,当△A′DC为等腰三角形时,AP的长为( )

A. 2B.
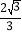 C. 2或
C. 2或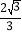 D. 2或
D. 2或
相关试题

