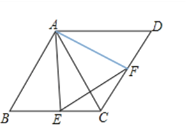
【题目】菱形ABCD中,∠B=60°,点E,F分别是BC,CD上的两个动点,且始终保持∠AEF=60°.
(1)试判断△AEF的形状并说明理由;
(2)若菱形的边长为2,求△ECF周长的最小值.
参考答案:
【答案】(1)△AEF是等边三角形,理由详见解析;(2)2+![]()
【解析】
(1)先根据四边形ABCD是菱形判断出△ABC的形状,再由ASA定理得出△AGE≌△ECF,故可得出AE=AF,由此可得出结论;
(2)根据垂线段最短可知当AE⊥BC时△ECF周长最小,由直角三角形的性质求出AE的长,故可得出结论.
解:(1)△AEF是等边三角形,理由是:
∵四边形ABCD是菱形,
∴AB=BC
∵∠B=60°.
∴△ABC是等边三角形,
在AB上截取BG=BE,则△BGE是等边三角形
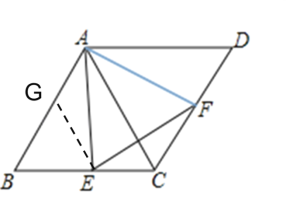
∴AG=AB-BG=BC-BE=EC,
∵∠AEC=∠BAE+∠B=∠AEF+∠FEC,又因为∠B=∠AEF=60°
∴∠BAE=∠CEF.
在△AGE与△ECF中,
∠AGE=∠ECF=120°,AG=EC,∠GAE=∠CEF
∴△AGE≌△ECF(ASA),
∴AE=EF.
∵∠AEF=60°,
∴△AEF是等边三角形.
(2)由(1)知△AEF是等边三角形,△AGE≌△ECF
所以CF=GE=BE,CF+EC=BC=定值=2
∵垂线段最短,
∴当AE⊥BC时,AE=EF最小,此时△ECF周长最小、
∵BC=2,∠B=60°,
∴AE=![]() ,
,
△ECF周长的最小值=2+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC和△CDE是以C为公共顶点的两个三角形.
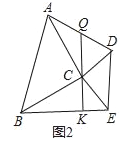
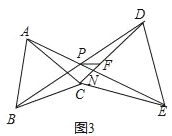
(1)如图1,当△ABC和△CDE都是等边三角形时,连接BD、AE相交于点P.求∠DPE的度数;
(2)如图2,当△ABC和△CDE都是等腰直角三角形,且∠ACB=∠DCE=90°时,连接AD、BE,Q为AD中点,连接QC并延长交BE于K.求证:QK⊥BE;
(3)在(1)的条件下,N是线段AE与CD的交点,PF是∠DPE的平分线,与DC交于点F,CN=2
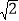 ,∠PFN=45°,求FN的长.
,∠PFN=45°,求FN的长.
-
科目: 来源: 题型:
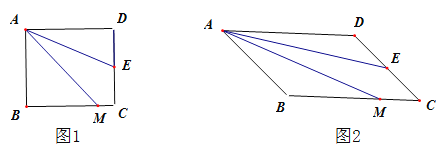
查看答案和解析>>【题目】如图,四边形ABCD是矩形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)证明:AM=AD+MC.
(2)若四边形ABCD是平行四边形,其它条件不变,如图,(1)中的结论是否成立?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在完成第10章的学习后,遇到了一些问题,请你帮助他.
(1)图1中,当
 ,试说明
,试说明 .
.(2)图2中,若
 ,则
,则 吗?请说明理由.
吗?请说明理由.(3)图3中,
 ,若
,若 ,
, ,
, ,
, ,则
,则 ______(直接写出结果,用含x,y,z的式子表示)
______(直接写出结果,用含x,y,z的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,BC=4,P为边AD上一动点,连接BP,把△ABP沿BP折叠,使A落在A′处,当△A′DC为等腰三角形时,AP的长为( )

A. 2B.
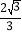 C. 2或
C. 2或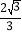 D. 2或
D. 2或
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为_________.

-
科目: 来源: 题型:
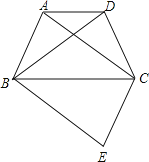
查看答案和解析>>【题目】如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
(1)求证:四边形ABEC是平行四边形.
(2)若AD=CD=6,∠ADC=120°,求四边形ABEC的面积.
相关试题

