【题目】在直角坐标系中,已知点A,B的坐标是(a,0),(b,0).a,b满足方程组![]() ,C为y轴正半轴上一点,且S△ABC=6.
,C为y轴正半轴上一点,且S△ABC=6.
(1)求A,B,C三点的坐标;
(2)是否存在点P(t,t),使S△PAB=![]() S△ABC?若存在,请求出P点的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出P点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)A(﹣3,0),B(1,0),C(0,3).(2)P(1,1)或(﹣1,﹣1).
【解析】
试题分析:(1)解出方程组即可得到时点A,B的坐标,利用S△ABC=6,求出点C的坐标;
(2)利用S△PAB=![]() S△ABC求出点P的坐标即可.
S△ABC求出点P的坐标即可.
解:(1)由方程组![]() ,
,
解得![]() ,
,
∴A(﹣3,0),B(1,0),
∵c为y轴正半轴上一点,且S△ABC=6,
∴![]() ABOC=6,解得:OC=3
ABOC=6,解得:OC=3
∴C(0,3).
(2)存在.
理由:∵P(t,t),且S△PAB=![]() S△ABC,
S△ABC,
∴![]() ×4×|t|=
×4×|t|=![]() ×6,
×6,
解得t=±1,
∴P(1,1)或(﹣1,﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼。小丽在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,根据图中提供的信息,解答下列各题:
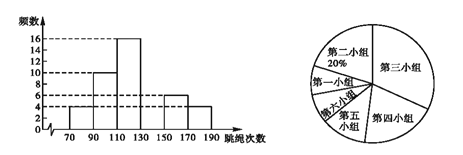
(1)本次调查共抽取了多少名学生?
(2)补全频数分布直方图;
(3)若全校共有1200名学生,跳绳成绩为优秀的约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】悠悠食品店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售的总份数不变,这两种菜品一天的总利润是316元.求A种菜品每天销售多少份?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80 m,DE=10 m,求障碍物B,C两点间的距离.(结果精确到0.1 m)(参考数据:
 ≈1.414,、
≈1.414,、 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个点在第一象限及
 轴、
轴、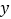 轴上运动,在第一秒钟,它从原点
轴上运动,在第一秒钟,它从原点 运动到
运动到 ,然后接着按图中箭头所示方向运动,即
,然后接着按图中箭头所示方向运动,即 →
→ →
→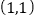 →
→ ,…,且每秒移动一个单位,到
,…,且每秒移动一个单位,到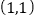 用时2秒,到
用时2秒,到 点用时6秒,到
点用时6秒,到 点用时12秒,…,那么到
点用时12秒,…,那么到 点用时________秒,第931秒时这个点所在位置坐标是_________.
点用时________秒,第931秒时这个点所在位置坐标是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,点
 、
、 、
、 均在格点上.
均在格点上.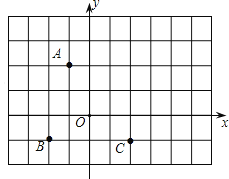
(1)请直接写出点
 、
、 、
、 的坐标分别为_________,_________,_________.
的坐标分别为_________,_________,_________.(2)若平移线段
 ,使
,使 移动到
移动到 的位置,请在图中画出
的位置,请在图中画出 移动后的位置
移动后的位置 ,依次连接
,依次连接 ,
, ,
, ,
, ,则四边形
,则四边形 的面积为________.
的面积为________.
相关试题

