Question

【题目】如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80 m，DE=10 m，求障碍物B，C两点间的距离．(结果精确到0.1 m)（参考数据： ≈1.414，、≈1.732）

Answer 1

【答案】障碍物B，C两点间的距离约为52.7m.

【解析】试题分析：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．通过解直角△AFD得到DF的长度；通过解直角△DCE得到CE的长度，则BC=BE-CE．

试题解析：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．

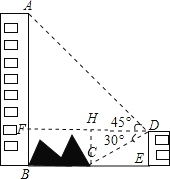
则DE=BF=CH=10m，

在直角△ADF中，∵AF=80m-10m=70m，∠ADF=45°，

∴DF=AF=70m．

在直角△CDE中，∵DE=10m，∠DCE=30°，

∴CE=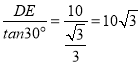（m），

∴BC=BE-CE=70-10≈70-17.32≈52.7（m）．

答：障碍物B，C两点间的距离约为52.7m．