【题目】模型建立:如图1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)模型应用:
①已知直线l1:![]() 与y轴交于
与y轴交于![]() 点,将直线l1绕着
点,将直线l1绕着![]() 点顺时针旋转45°至l2,如图2,求l2的函数解析式;
点顺时针旋转45°至l2,如图2,求l2的函数解析式;
②如图3,长方形ABCO,![]() 为坐标原点,
为坐标原点,![]() 的坐标为(8,6),
的坐标为(8,6),![]() 、
、![]() 分别在坐标轴上,
分别在坐标轴上,![]() 是线段
是线段![]() 上动点,点
上动点,点![]() 是直线
是直线![]() 上的一点,若△APD是以点D为直角顶点的等腰Rt△,请直接写出点
上的一点,若△APD是以点D为直角顶点的等腰Rt△,请直接写出点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)见解析;(2)①![]() ;②(-6,8)或(-2,0).
;②(-6,8)或(-2,0).
【解析】
(1)先根据△ABC为等腰直角三角形得出CB=CA,再由AAS定理可得△ACD≌△CBE,由全等三角形的性质可得![]() ;
;
(2)①如图2中,设直线l1交x轴于B,作BP⊥AC于P,作PE⊥OB于E,PF⊥y轴于F.首先证明四边形PEOF是正方形,求出点P的坐标,利用待定系数法即可解决问题.
②当点D为直角顶点,分点D在直线PA的上方或下方两种情况,如图3所示,当点D′在直线PA上方时,∠A D′P=90°时,A D′=P D′,设D′(x,-2x-4),利用三角形全等得到-2x-10=x+8,x=-6,OF=-2x-4 =8,即可得出结论;同理,再求出点D在直线PA下方时点![]() 的坐标.
的坐标.
(1)证明:如图1中,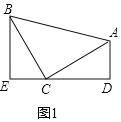
∵△ABC为等腰直角三角形,
∴BC=CA,∠ACD+∠BCE=90°,
又∵AD⊥ED,BE⊥ED,
∴∠D=∠E=90°,∠EBC+∠BCE=90°,
∴∠ACD=∠EBC,
在△ACD与△CBE中,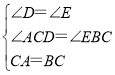 ,
,
∴△ACD≌△CBE(AAS);
∴![]() ;
;
(2)①如图2中,设直线l1交x轴于B,作BP⊥AC于P,作PE⊥OB于E,PF⊥y轴于F.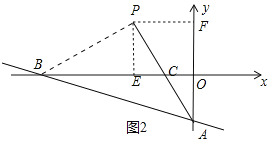
由(1)可知△PBE≌△PAF,
∴BE=AF,PE=PF,设PE=PF=a,
∵∠PEO=∠EOF=∠PFO=90°,
∴四边形PEOF是矩形,
∵PE=PF,
∴四边形PEOF是正方形,
∴OE=OF=a,
∵![]() =0时,x=-28,;x=0时,y=-4,
=0时,x=-28,;x=0时,y=-4,
∴B(-28,0),A(0,-4),
∴a+4+a=28,
∴a=12,
∴P(-12,12),设直线l2的解析式为y=kx+b则有![]() ,
,
解得 ,
,
∴直线l2的解析式为![]() ;
;
②如图3中,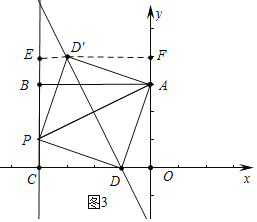
当点D位于直线![]() 上,点D为直角顶点时,分两种情况,
上,点D为直角顶点时,分两种情况,
当点D′在直线PA上方时,过D′作x轴的平行线EF,交直线OA于F,交直线BC于E,设D′(x,-2x-4);
则OF=-2x-4,AF=(-2x-4)-6=-2x-10,D′E=EF-D′F=x+8;
由(1)可知△AD′F≌△D′PE,得D′E=AF,即:
-2x-10=x+8,x=-6,OF=-2x-4 =8,
∴D′(-6,8);
当点D在直线PA下方时,同理可得D(-2,0),
综上所述,满足条件的点D的坐标为(-6,8)或(-2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速
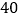 千米/时,已知交警测速点
千米/时,已知交警测速点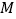 到该公路
到该公路 点的距离为
点的距离为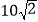 米,
米,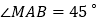 ,
,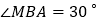 (如图所示),现有一辆汽车由
(如图所示),现有一辆汽车由 往
往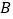 方向匀速行驶,测得此车从
方向匀速行驶,测得此车从 点行驶到
点行驶到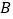 点所用的时间为
点所用的时间为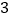 秒.
秒.
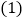 求测速点
求测速点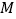 到该公路的距离;
到该公路的距离;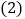 通过计算判断此车是否超速.(参考数据:
通过计算判断此车是否超速.(参考数据: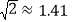 ,
,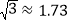 ,
,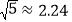 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求(1)求直线AE的函数表达式;(2)求D点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1的解析表达式为y=-
 x-1,且l1与x轴交于点D,直线l2经过定点A(2,0),B(-1,3),直线l1与l2交于点C.
x-1,且l1与x轴交于点D,直线l2经过定点A(2,0),B(-1,3),直线l1与l2交于点C.
(1)求直线l2的函数关系式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,A、B两个顶点在
 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A.
 B.
B.  C.
C.  D.
D. 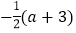
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,BE⊥AC于点E,点D在AC上,且AD=AB,AK平分∠CAB,交线段BE于点F,交边CB于点K.
(1)在图中找出一对全等三角形,并证明;
(2)求证:FD∥BC .

-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)求证:△ABE≌△ACD;
(2)求证:DC⊥BE.

相关试题

