【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求(1)求直线AE的函数表达式;(2)求D点的坐标.

参考答案:
【答案】(1)![]() ;(2)D(0,5).
;(2)D(0,5).
【解析】
(1)先根据勾股定理求出BE的长,进而可得出CE的长,求出E点坐标,根据点A、E的坐标即可求直线AE的函数表达式;
(2)在Rt△DCE中,由DE=OD及勾股定理可求出OD的长,进而得出D点坐标.
解:(1)∵将矩形纸片沿AD翻折,使点O落在BC边上的点E处,
∴在Rt△ABE中,AE=AO=10,AB=8,BE=![]() =
=![]() =6,
=6,
∴CE=BC-BE=10-6=4,
∴E(4,8),
∵点A在x轴的正半轴上,OA=10,
∴A(10,0),
设直线AE的函数表达式为y=kx+b,
则![]() ,解得:
,解得: ,
,
∴直线AE的函数表达式为:![]() ;
;
(2)在Rt△DCE中,DC2+CE2=DE2,
∵DE=OD,CD=8-OD,
∴(8-OD)2+42=OD2,
解得:OD=5,
∴D(0,5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市准备在相距
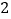 千米的
千米的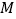 ,
, 两工厂间修一条笔直的公路,但在
两工厂间修一条笔直的公路,但在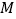 地北偏东
地北偏东 方向、
方向、 地北偏西
地北偏西 方向的
方向的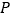 处,有一个半径为
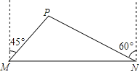
处,有一个半径为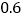 千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:
千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据: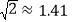 ,
,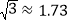 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,埃航
 客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下
客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下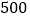 米的
米的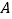 点处测得俯角为
点处测得俯角为 的前下方海底有黑匣子信号发出,继续沿原方向直线航行
的前下方海底有黑匣子信号发出,继续沿原方向直线航行 米后到达
米后到达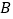 点,在
点,在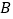 处测得俯角为
处测得俯角为 的前下方海底有黑匣子信号发出,求海底黑匣子
的前下方海底有黑匣子信号发出,求海底黑匣子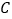 点距离海面的深度(结果保留根号).
点距离海面的深度(结果保留根号).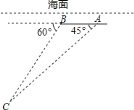
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速
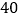 千米/时,已知交警测速点
千米/时,已知交警测速点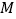 到该公路
到该公路 点的距离为
点的距离为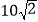 米,
米,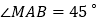 ,
,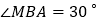 (如图所示),现有一辆汽车由
(如图所示),现有一辆汽车由 往
往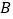 方向匀速行驶,测得此车从
方向匀速行驶,测得此车从 点行驶到
点行驶到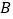 点所用的时间为
点所用的时间为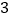 秒.
秒.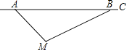
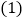 求测速点
求测速点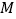 到该公路的距离;
到该公路的距离;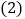 通过计算判断此车是否超速.(参考数据:
通过计算判断此车是否超速.(参考数据: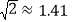 ,
,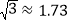 ,
,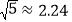 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1的解析表达式为y=-
 x-1,且l1与x轴交于点D,直线l2经过定点A(2,0),B(-1,3),直线l1与l2交于点C.
x-1,且l1与x轴交于点D,直线l2经过定点A(2,0),B(-1,3),直线l1与l2交于点C.
(1)求直线l2的函数关系式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】模型建立:如图1,等腰直角三角形
 中,
中, ,
, ,直线
,直线 经过点
经过点 ,过
,过 作
作 于
于 ,过
,过 作
作 于
于 .
.(1)求证:
 ;
;(2)模型应用:
①已知直线l1:
 与y轴交于
与y轴交于 点,将直线l1绕着
点,将直线l1绕着 点顺时针旋转45°至l2,如图2,求l2的函数解析式;
点顺时针旋转45°至l2,如图2,求l2的函数解析式;②如图3,长方形ABCO,
 为坐标原点,
为坐标原点, 的坐标为(8,6),
的坐标为(8,6), 、
、 分别在坐标轴上,
分别在坐标轴上, 是线段
是线段 上动点,点
上动点,点 是直线
是直线 上的一点,若△APD是以点D为直角顶点的等腰Rt△,请直接写出点
上的一点,若△APD是以点D为直角顶点的等腰Rt△,请直接写出点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,A、B两个顶点在
 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A.
 B.
B.  C.
C.  D.
D. 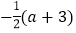
相关试题

