【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)求证:△ABE≌△ACD;
(2)求证:DC⊥BE.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据等腰直角三角形的性质,可以得出△ABE≌△ACD;
(2)由△ABE≌△ACD可以得出∠B=∠ACD﹣45°,进而得出∠DCB=90°,就可以得出结论.
证明:(1)∵△ABC与△AED均为等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°.∠ABC=∠ACB=45°,
∴∠BAC+∠CAE=∠EAD+∠CAE.
即∠BAE=∠CAD,
在△ABE与△ACD中,
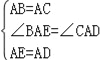 ,
,
∴△ABE≌△ACD(SAS),
(2)证明:∵△ABE≌△ACD,
∴∠ACD=∠ABE=45°,
又∵∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴DC⊥BE.
点睛:此题主要考查了等腰直角三角形的性质以及全等三角形的性质与判定,根据等腰三角形的性质得出AC=AB,AD=AE,利用SAS证全等是解题关键.
-
科目: 来源: 题型:
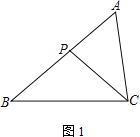
查看答案和解析>>【题目】在△ABC中,P为边AB上一点.
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
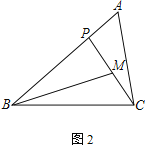
(2) 若M为CP的中点,AC=2,
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
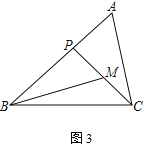
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC于D,若BD=AD,FD=CD.猜想:BF与AC的关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.(10分)

(1)请在图中画出平移后的△A′B′C′。
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级400名学生到郊外参加植树活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金150元,大客车每辆租金250元,请选出最省线的租车方案,并求出最少租金.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.

(1)当点E为AB的中点时(如图1),则有AE DB(填“>”“<”或“=”);
(2)猜想AE与DB的数量关系,并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究应用:用“∪”、“∩”定义两种新运算:对于两数a、b,规定a∪b=10a×10b,a∩b=10a÷10b,例如:3∪2=103×102=105,3∩2=103÷102=10.
(1) 求: (2017∪983) 的值
(2) 求: (2018∩2016) 的值;
(3) 当x为何值时, (x∪5)的值与 (23∩17)的值相等.
相关试题

