搜索
【题目】如图,△ABC中，A、B两个顶点在
轴的上方,点C的坐标是(1，0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a，则点B的横坐标是( )
A. 
B. 
C. 
D. 
参考答案：
【答案】D
【解析】
△A′B′C的边长是△ABC的边长的2倍，过B点和B′点作x轴的垂线，垂足分别是D和E，因为点B′的横坐标是a，则EC=a+1．可求DC=
（a+1），则B点的横坐标是-（a+1）-1= (a+3)．
过B点和B′点作x轴的垂线，垂足分别是D和E
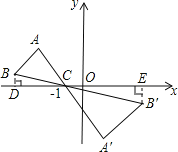
∵点B′的横坐标是a，点C的坐标是（-1，0）．
∴EC=a+1
又∵△A′B′C的边长是△ABC的边长的2倍
∴DC=（a+1）
∴DO=（a+3）
∴B点的横坐标是 (a+3)
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8．在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求（1）求直线AE的函数表达式；（2）求D点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线l1的解析表达式为y=-
x-1，且l1与x轴交于点D，直线l2经过定点A（2，0），B（-1，3），直线l1与l2交于点C．
（1）求直线l2的函数关系式；
（2）求△ADC的面积；
（3）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请写出点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】模型建立：如图1，等腰直角三角形
中，
，
，直线
经过点
，过
作
于
，过
作
于
．（1）求证：
；（2）模型应用：
①已知直线l1：
与y轴交于点，将直线l1绕着点顺时针旋转45°至l2，如图2，求l2的函数解析式；②如图3，长方形ABCO，
为坐标原点，的坐标为（8，6），、分别在坐标轴上，
是线段
上动点，点是直线
上的一点，若△APD是以点D为直角顶点的等腰Rt△，请直接写出点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ABC=90°，BE⊥AC于点E，点D在AC上，且AD＝AB，AK平分∠CAB，交线段BE于点F，交边CB于点K．
（1）在图中找出一对全等三角形，并证明；
（2）求证：FD∥BC ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连结DC．
（1）求证：△ABE≌△ACD；
（2）求证：DC⊥BE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，△ABC是等边三角形，D点是AC的中点，延长BC到E，使CE=CD．
（1）用尺规作图的方法，过D点作DM⊥BE，垂足是M（不写作法，保留作图痕迹）；
（2）求证：BM=EM．
相关试题
