【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y= ![]() 的大致图象是( )
的大致图象是( ) 
A.
B.
C.
D.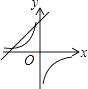
参考答案:
【答案】C
【解析】解:∵抛物线开口向下, ∴a<0.
∵抛物线与y轴的交点在y轴正半轴,
∴c>0.
∴抛物线的对称轴在x轴正半轴,
∴﹣ ![]() >0,
>0,
∴b>0,
∵一次函数y=ax+b的图象经过一二四象限,反比例函数y= ![]() 的图象的两个分支分别位于一三象限.
的图象的两个分支分别位于一三象限.
故选C.
【考点精析】本题主要考查了一次函数的图象和性质和反比例函数的图象的相关知识点,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A路口的交通信号灯依次显示为红灯亮20秒,绿灯亮40秒,再红灯亮20秒,绿灯亮40秒,如此连续不断循环显示下去…
(1)求A路口显示红灯的概率.
(2)小亮上班路上会遇到A,B两个路口,B路口红绿灯的显示方式和A路口完全相同,求他在上班路上两次都遇到红灯的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图的抛物线是把抛物线y=
 x2平移后经过(0,﹣1)和(4,﹣1)两点得到的.
x2平移后经过(0,﹣1)和(4,﹣1)两点得到的. 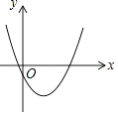
(1)求平移后抛物线的表达式.
(2)求平移后方向和距离.
(3)在平移后的抛物线上取一点P,以P为圆心作半径为2的⊙P,当⊙P与y轴相切时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线y=
 x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;
(ii)取BC的中点N,连接NP,BQ.试探究 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角三角形ABC中,BD⊥AC于D,CE⊥AB于E,且S△ADE=
 S四边形BEDC , 则∠A=( )
S四边形BEDC , 则∠A=( )
A.75°
B.60°
C.45°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.
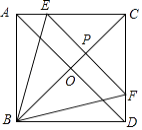
(1)求tan∠ABE的值.
(2)求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知y=﹣x+m(m>4)过动点A(m,0),并与反比例函数y=
 的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=
的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=  的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D.
的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D. 
(1)当m=5时,求B、C两点的坐标.
(2)求证:无论m取何值,线段DE的长始终为定值.
(3)记点C关于直线DE的对称点为C′,当四边形CDC′E为菱形时,求m的值.
相关试题

