【题目】如图,已知y=﹣x+m(m>4)过动点A(m,0),并与反比例函数y= ![]() 的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=
的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y= ![]() 的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D.
的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D. 
(1)当m=5时,求B、C两点的坐标.
(2)求证:无论m取何值,线段DE的长始终为定值.
(3)记点C关于直线DE的对称点为C′,当四边形CDC′E为菱形时,求m的值.
参考答案:
【答案】
(1)解:把m=5代入y=﹣x+m中得:y=﹣x+5,
则  解得:
解得: ![]() ,
, ![]() ,
,
∴B(1,4),C(4,1);
(2)解:如图1,连接OD、AD,
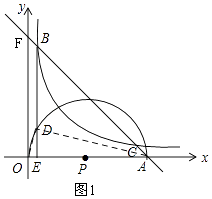
∵A(m,0),
∴OA=m,
y=﹣x+m中,当x=0时,y=m,则F(0,m),
∴OF=m,
∴△AOF是等腰直角三角形,
∴∠OAB=45°,
∵BE⊥OA,
∴△ABE是等腰直角三角形,
∴BE=AE,
∵OA是⊙P的直径,
∴∠ODA=90°,
∵∠ODE=∠OAD,
∵∠OED=∠DEA=90°,
∴△ODE∽△DAE,
∴ ![]() ,
,
∴DE2=OEAE=OEBE,
∵B是反比例函数上的点,即OEBE=4
∴无论m取何值,线段DE的长始终为定值;
(3)解:如图3,连接CC′,设DE与CC′交于G,

由(2)得:DE2=4,
∴DE=2,
∵四边形CDC′E为菱形,
∴DG=EG=1,
∴C的纵坐标为1,
当y=1时, ![]() =1,x=4,
=1,x=4,
∴C(4,1),
把C(4,1)代入y=﹣x+m中得:﹣4+m=1,
m=5.
【解析】(1)把M=5代入一次函数解析式中,与反比例函数列方程组解出即可;(2)作辅助线,如图1,证明△ODE∽△DAE,列比例式得: ![]() ,则DE2=OEAE=OEBE=4,所以线段DE的长始终为定值;(3)根据菱形的性质求出C的坐标,代入一次函数的解析式中可得m的值.
,则DE2=OEAE=OEBE=4,所以线段DE的长始终为定值;(3)根据菱形的性质求出C的坐标,代入一次函数的解析式中可得m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=
 的大致图象是( )
的大致图象是( ) 
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角三角形ABC中,BD⊥AC于D,CE⊥AB于E,且S△ADE=
 S四边形BEDC , 则∠A=( )
S四边形BEDC , 则∠A=( )
A.75°
B.60°
C.45°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.
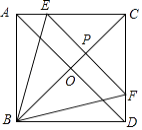
(1)求tan∠ABE的值.
(2)求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中∠C=90°,∠A=30°,BC=2,点P,Q,R分别是AB,AC,BC上的动点,PQ+PR+QR的最小值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上一点.
(1)求证:AD2+DB2=ED2;
(2)若BC=
 ,求四边形ADCE的面积.
,求四边形ADCE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有两条边长的比值为
 的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
(1)设“潜力三角形”较短直角边长为a,斜边长为c,请你直接写出 的值为;
的值为;
(2)若∠AED=∠DCB,求证:△BDF是“潜力三角形”;
(3)若△BDF是“潜力三角形”,且BF=1,求线段AC的长.
相关试题

