【题目】在锐角三角形ABC中,BD⊥AC于D,CE⊥AB于E,且S△ADE= ![]() S四边形BEDC , 则∠A=( )
S四边形BEDC , 则∠A=( )
A.75°
B.60°
C.45°
D.30°
参考答案:
【答案】B
【解析】解:如图,连接DE. 
∵BD⊥AC于D,CE⊥AB于E,
∴∠AEC=∠ADB=90°,
∵∠A=∠A,
∴△ABD∽△ACE,
∴ ![]() ,
,
∴ ![]() ,∵∠A=∠A,
,∵∠A=∠A,
∴△AED∽△ACB,
∵S△ADE= ![]() S四边形BEDC
S四边形BEDC
∴S△ADE:S△ABC=1:4
∴( ![]() )2=
)2= ![]() ,
,
∴AC=2AE,
∴sin∠ACE= ![]() ,
,
∴∠ACE=30°,
∴∠A=90°﹣∠ACE=60°,
故选B.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的抛物线是把抛物线y=
 x2平移后经过(0,﹣1)和(4,﹣1)两点得到的.
x2平移后经过(0,﹣1)和(4,﹣1)两点得到的. 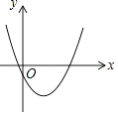
(1)求平移后抛物线的表达式.
(2)求平移后方向和距离.
(3)在平移后的抛物线上取一点P,以P为圆心作半径为2的⊙P,当⊙P与y轴相切时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线y=
 x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;
(ii)取BC的中点N,连接NP,BQ.试探究 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=
 的大致图象是( )
的大致图象是( ) 
A.
B.
C.
D.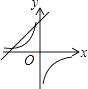
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.
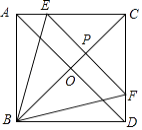
(1)求tan∠ABE的值.
(2)求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知y=﹣x+m(m>4)过动点A(m,0),并与反比例函数y=
 的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=
的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=  的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D.
的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D. 
(1)当m=5时,求B、C两点的坐标.
(2)求证:无论m取何值,线段DE的长始终为定值.
(3)记点C关于直线DE的对称点为C′,当四边形CDC′E为菱形时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中∠C=90°,∠A=30°,BC=2,点P,Q,R分别是AB,AC,BC上的动点,PQ+PR+QR的最小值是_____.

相关试题

