【题目】如图的抛物线是把抛物线y= ![]() x2平移后经过(0,﹣1)和(4,﹣1)两点得到的.
x2平移后经过(0,﹣1)和(4,﹣1)两点得到的. 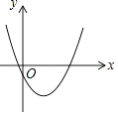
(1)求平移后抛物线的表达式.
(2)求平移后方向和距离.
(3)在平移后的抛物线上取一点P,以P为圆心作半径为2的⊙P,当⊙P与y轴相切时,求点P的坐标.
参考答案:
【答案】
(1)解:设平移后的抛物线的解析式为y= ![]() x2+bx+c,
x2+bx+c,
把(0,﹣1)和(4,﹣1)两点代入
y= ![]() x2+bx+c,得,
x2+bx+c,得, ![]() ,
,
解得: ![]() ,
,
∴平移后抛物线的表达式为:y= ![]() x2﹣2x﹣1;
x2﹣2x﹣1;
(2)解:∵y= ![]() x2﹣2x﹣1=
x2﹣2x﹣1= ![]() (x﹣2)2﹣3,
(x﹣2)2﹣3,
∴把y= ![]() x2向右平移2个单位,向下平移3个单位即可;
x2向右平移2个单位,向下平移3个单位即可;
(3)解:∵点P在抛物线y= ![]() x2﹣2x﹣1上,⊙P与y轴相切时,
x2﹣2x﹣1上,⊙P与y轴相切时,
∴设P(a,2)或(a,﹣2),
把P(2,a)代入y= ![]() x2﹣2x﹣1得a=
x2﹣2x﹣1得a= ![]() ×22﹣2×2﹣1,
×22﹣2×2﹣1,
∴a=﹣3,
∴P(2,﹣3),
把P(﹣2,a)代入y= ![]() x2﹣2x﹣1得a=
x2﹣2x﹣1得a= ![]() ×(﹣2)2﹣2×(﹣2)﹣1,
×(﹣2)2﹣2×(﹣2)﹣1,
∴a=5,
∴P(2,5),
综上所述:以P为圆心作半径为2的⊙P,当⊙P与y轴相切时,点P的坐标为(2,﹣3)或(﹣2,5).
【解析】(1)设平移后的抛物线的解析式为y= ![]() x2+bx+c,把(0,﹣1)和(4,﹣1)两点代入y=
x2+bx+c,把(0,﹣1)和(4,﹣1)两点代入y= ![]() x2+bx+c,解方程组即可得到结论;(2)把y=
x2+bx+c,解方程组即可得到结论;(2)把y= ![]() x2﹣2x﹣1配方得到y=
x2﹣2x﹣1配方得到y= ![]() (x﹣2)2﹣3,于是得到结论;(3)当⊙P与y轴相切时,点P的横坐标是2或﹣2,把点P的坐标代入函数解析式,即可求得相应的纵坐标.
(x﹣2)2﹣3,于是得到结论;(3)当⊙P与y轴相切时,点P的横坐标是2或﹣2,把点P的坐标代入函数解析式,即可求得相应的纵坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了减轻学生课业负担,提高课堂效果,我县教体局积极推进 “高效课堂”建设.
某学校的《课堂检测》印刷任务原来由甲复印店承接,其每月收费y(元)与复印页数x(页)的函数关系如图所示:
⑴从图象中可看出:每月复印超过500页部分每页收费 元;
⑵现在乙复印店表示:若学校先按每月付给200元的月承包费,则可按每页0.15元收费.乙复印店每月收费y(元)与复印页数x(页)的函数关系为 ;
⑶在给出的坐标系内画出(2)中的函数图象,并结合函数图象回答每月复印在3000页左右应选择哪个复印店?

-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD内部,∠B=50°,∠D=30°,求∠BPD.
(2)如图2,将点P移到AB、CD外部,则∠BPD、∠B、∠D之间有何数量关系?(不需证明)
(3)如图3,写出∠BPD﹑∠B﹑∠D﹑∠BQD之间的数量关系?请证明你的结论.
(4)如图4,求出∠A+∠B+∠C+∠D+∠E+∠F的度数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】A路口的交通信号灯依次显示为红灯亮20秒,绿灯亮40秒,再红灯亮20秒,绿灯亮40秒,如此连续不断循环显示下去…
(1)求A路口显示红灯的概率.
(2)小亮上班路上会遇到A,B两个路口,B路口红绿灯的显示方式和A路口完全相同,求他在上班路上两次都遇到红灯的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线y=
 x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;
(ii)取BC的中点N,连接NP,BQ.试探究 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=
 的大致图象是( )
的大致图象是( ) 
A.
B.
C.
D.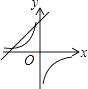
-
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角三角形ABC中,BD⊥AC于D,CE⊥AB于E,且S△ADE=
 S四边形BEDC , 则∠A=( )
S四边形BEDC , 则∠A=( )
A.75°
B.60°
C.45°
D.30°
相关试题

