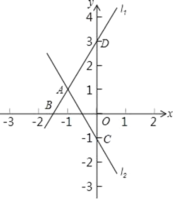
【题目】已知直线l1:y1=2x+3与直线l2:y2=kx﹣1交于A点,A点横坐标为﹣1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
(1)求出A、B、C、D点坐标;
(2)求出直线l2的解析式;
(3)连结BC,求出S△ABC.
参考答案:
【答案】(1)A(﹣1,1),B(﹣1.5,0),D(0,3),C(0,﹣1);(2)y2=﹣2x﹣1;(3)1.
【解析】
(1)根据直线及坐标的特点即可分别求解;
(2)把A(﹣1,1)代入y2=kx﹣1即可求解;
(3)利用S△ABC=S△ABE+S△BCE即可求解.
解:(1)把x=﹣1代入y1=2x+3,得:y=1,即A(﹣1,1),
对于y1=2x+3,
令x=0,得到y=3;令y=0,得到x=﹣1.5,
∴B(﹣1.5,0),D(0,3),
把A(﹣1,1)代入y2=kx﹣1得:k=﹣2,即y2=﹣2x﹣1,
令x=0,得到y=﹣1,即C(0,﹣1);
(2)把A(﹣1,1)代入y2=kx﹣1得:k=﹣2,
则y2=﹣2x﹣1;
(3)连接BC,设直线l2与x轴交于点E,如图所示,
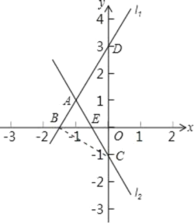
对于y2=﹣2x﹣1,令y=0,得到x=﹣0.5,即OE=0.5,
∴BE=OB﹣OE=1.5﹣0.5=1,
则S△ABC=S△ABE+S△BCE=![]() ×1×1+
×1×1+![]() ×1×1=1.
×1×1=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点D,且l∥BC
(1)求证:AD平分∠BAC
(2)作∠ABC的平分线BE交AD于点E,求证:BD=DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧
 于点P,Q,且点P, Q在AB异侧,连接OP.
于点P,Q,且点P, Q在AB异侧,连接OP.(1)求证:AP=BQ;
(2)当BQ=4
 时,求扇形COQ的面积及
时,求扇形COQ的面积及 的长(结果保留π);
的长(结果保留π);(3)若△APO的外心在扇形COD的内部,请直接写出OC的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y =ax2+bx+ c的图象如图,有以下结论:①a+b+c<0; ②a-b+c >2;③abc>0;④4a-2b+c <0;⑤c-a>1.其中所有正确结论的序号是( )

A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠C=α,∠EAC+∠FBC=β
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则α与β有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与α、β的关系是______.(用α、β表示)
(3)如图③,若α≥β,∠EAC与∠FBC的平分线相交于P1,∠EAP1与∠FBP1的平分线交于P2 ;依此类推,则∠P5=______.(用α、β表示)



-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是黄金分割比(黄金分割比0.618)著名的“断臂维纳斯”便是如此.此外最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是黄金分割比.若某人满足上述两个黄金分割比例,且腿长为103cm,头顶至脖子下端的长度为25cm,则其身高可能是( )

A.165cmB.170cmC.175cmD.180cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:(1)函数
 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;(2)下表是x与y的几组对应值.

...





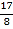

1
2
3
...

...









m
...
求m的值;
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,
 ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可).
相关试题

