【题目】如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点D,且l∥BC
(1)求证:AD平分∠BAC
(2)作∠ABC的平分线BE交AD于点E,求证:BD=DE.

参考答案:
【答案】证明见解析
【解析】
(1)连接OD,由直线l与⊙O相切于点D可得出OD⊥l,结合l∥BC即可得出OD⊥BC,再根据垂径定理即可得出![]() ,进而可得出∠BAD=∠CAD,即AD平分∠BAC;
,进而可得出∠BAD=∠CAD,即AD平分∠BAC;
(2)由角平分线的定义结合(1)的结论即可得出∠CBD+∠CBE=∠BAE+∠ABE,再根据三角形外角的性质即可得出∠EBD=∠DEB,由此即可证出BD=DE.
(1)连接OD,如图所示.
∵直线l与⊙O相切于点D,
∴OD⊥l.
∵l∥BC,
∴OD⊥BC,
∴![]() ,
,
∴∠BAD=∠CAD,
∴AD平分∠BAC;
(2)∵BE平分∠ABC,
∴∠ABE=∠CBE.
又∵![]() ,
,
∴∠BAD=∠CBD,
∴∠CBD+∠CBE=∠BAE+∠ABE.
又∵∠DEB=BAE+∠ABE,
∴∠EBD=∠DEB,
∴BD=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数
空间与图形
统计与概率
综合与实践
学生甲
90
94
86
90
学生乙
94
82
93
91
(1)分别计算甲、乙成绩的平均数和方差;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P从
 出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
【答案】

【解析】
根据反射角与入射角的定义作出图形;由图可知,每6次反弹为一个循环组依次循环,用2018除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图所示:经过6次反弹后动点回到出发点
 ,
,
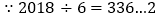 ,
, 当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹, 点P的坐标为
点P的坐标为 .
.故答案为:
 .
.【点睛】
此题主要考查了点的坐标的规律,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
【题型】填空题
【结束】
15【题目】为了保护环境,某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为
 万升;B种型号每辆价格为b万元,每年节省油量为
万升;B种型号每辆价格为b万元,每年节省油量为 万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元. 请求出a和b;
请求出a和b; 若购买这批混合动力公交车每年能节省
若购买这批混合动力公交车每年能节省 万升汽油,求购买这批混合动力公交车需要多少万元?
万升汽油,求购买这批混合动力公交车需要多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】我县古田镇某纪念品商店在销售中发现:“成功从这里开始”的纪念品平均每天可售出20件,每件盈利40元.为了扩大销售量,增加盈利,尽快减少库存,该商店在今年国庆黄金周期间,采取了适当的降价措施,改变营销策略后发现:如果每件降价4元,那么平均每天就可多售出8件.商店要想平均每天在销售这种纪念品上盈利1200元,那么每件纪念品应降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧
 于点P,Q,且点P, Q在AB异侧,连接OP.
于点P,Q,且点P, Q在AB异侧,连接OP.(1)求证:AP=BQ;
(2)当BQ=4
 时,求扇形COQ的面积及
时,求扇形COQ的面积及 的长(结果保留π);
的长(结果保留π);(3)若△APO的外心在扇形COD的内部,请直接写出OC的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y =ax2+bx+ c的图象如图,有以下结论:①a+b+c<0; ②a-b+c >2;③abc>0;④4a-2b+c <0;⑤c-a>1.其中所有正确结论的序号是( )

A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤
-
科目: 来源: 题型:
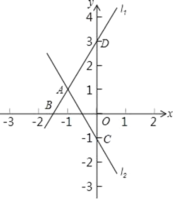
查看答案和解析>>【题目】已知直线l1:y1=2x+3与直线l2:y2=kx﹣1交于A点,A点横坐标为﹣1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
(1)求出A、B、C、D点坐标;
(2)求出直线l2的解析式;
(3)连结BC,求出S△ABC.
相关试题

