【题目】若∠C=α,∠EAC+∠FBC=β
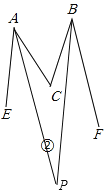
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则α与β有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与α、β的关系是______.(用α、β表示)
(3)如图③,若α≥β,∠EAC与∠FBC的平分线相交于P1,∠EAP1与∠FBP1的平分线交于P2 ;依此类推,则∠P5=______.(用α、β表示)



参考答案:
【答案】 ∠APB=α-![]() β ∠P5=α-
β ∠P5=α-![]() β
β
【解析】试题分析:(1)根据角平分线的定义表示出∠MAC+∠NCB,再根据两直线平行,内错角相等可得∠C=∠MAC+∠NBC;
(2)根据角平分线的定义表示出∠PAC+∠PBC,利用三角形的一个外角等于与它不相邻的两个内角的和列式整理即可得解;
(3)根据(2)的结论分别表示出∠P1、∠P2…,从而得解.
试题解析:
解:(1)∵AM是∠EAC的平分线,BN是∠FBC的平分线,
∴∠MAC+∠NCB=![]() ∠EAC+
∠EAC+![]() ∠FBC=
∠FBC=![]() β,
β,
∵AM∥BN,
∴∠C=∠MAC+∠NCB,
即α=![]() β;
β;
(2)∵∠EAC的平分线与∠FBC平分线相交于P,
∴∠PAC+∠PBC=![]() ∠EAC+
∠EAC+![]() ∠FBC=
∠FBC=![]() β,
β,
∴∠C=∠APB+(∠PAC+∠PBC),
∴α=∠APB+![]() β,
β,
即∠APB=α-![]() β;
β;
(3)由(2)得,∠P1=∠C-(∠PAC+∠PBC)=α-![]() β,
β,
∠P2=∠P1-(∠P2AP1+∠P2BP1),
=α-![]() β-
β-![]() β=α-
β=α-![]() β,
β,
∠P3=α-![]() β-
β-![]() β=α-
β=α-![]() β,
β,
∠P4=α-![]() β-
β-![]() β=α-
β=α-![]() β,
β,
∠P5=α-![]() β-
β-![]() β=α-
β=α-![]() β.
β.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,
(1)图①中,已知AF⊥BC , ∠B=500,∠C=600. 求∠DAF的度数.

(2)图②中,请你在直线AD上任意取一点E(不与点A、D重合),画EF⊥BC,垂足为F.已知∠B=α,∠C=β(β>a).求∠DEF的度数. (用α、β的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:1002-992+982-972+962-952+…+22-1;
(2)计算:
 .
.(3)因式分解:-4a2b+24ab-36b.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在折纸活动中,小明制作了一张⊿ABC纸片,点D、E分别是边AB、AC上,将⊿ABC沿着DE折叠压平,A与A’重合,若∠A=75°,则∠1+∠2=( )
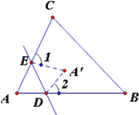
A. 150° B. 210° C. 105° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出△ABC的AB边上的中线CD;
(2)画出△ABC向右平移4个单位后得到的△A1B1C1;
(3)图中AC与A1C1的关系是: ;
(4)图中,能使S△ABQ=S△ABC的格点Q(点Q不与点C重合),共有 个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四个相同的小长方形,然后按图②的方式拼成一个正方形.
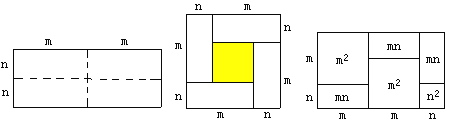
图① 图② 图③
(1)你认为图②中的阴影部分的正方形的边长等于________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①: ;
方法②: ;
(3)请你观察图②,利用图形的面积写出
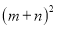 、
、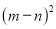 ,
, 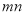 这三个代数式之间的等量关系: ;
这三个代数式之间的等量关系: ;(4)根据(3)中的结论,若
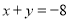 ,
, 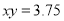 ,则
,则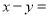 ;
;(5)有许多代数恒等式可以用图形的面积来表示.
如图③,它表示了
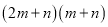
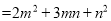 .
.试画出一个几何图形,使它的面积能表示:
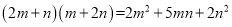
相关试题

