【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是x与y的几组对应值.
| ... |
|
|
|
|
|
|
| 1 | 2 | 3 | ... |
| ... |
|
|
|
|
|
|
|
|
| m | ... |
求m的值;
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,![]() ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可).
参考答案:
【答案】(1)x≠0;(2)![]() ;(3)画图见解析;(4)具体见解析.
;(3)画图见解析;(4)具体见解析.
【解析】试题分析:(1)由图表可知x≠0;
(2)根据图表可知当x=3时的函数值为m,把x=3代入解析式即可求得;
(3)根据坐标系中的点,用平滑的曲线连接即可;
(4)观察图象即可得出该函数的其他性质.
试题解析:(1)x≠0;
(2)当x=3 时,![]() ;
;
(3)注:要用平滑的曲线连接,图象不能与y轴相交;

(4)函数的性质有很多.如:
①当x<0时,y值随着x值的增大而减小;
②该函数没有最大值;
③该函数图象与y轴没有交点.
-
科目: 来源: 题型:
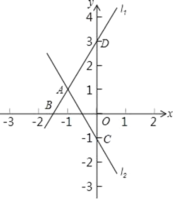
查看答案和解析>>【题目】已知直线l1:y1=2x+3与直线l2:y2=kx﹣1交于A点,A点横坐标为﹣1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
(1)求出A、B、C、D点坐标;
(2)求出直线l2的解析式;
(3)连结BC,求出S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠C=α,∠EAC+∠FBC=β
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则α与β有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与α、β的关系是______.(用α、β表示)
(3)如图③,若α≥β,∠EAC与∠FBC的平分线相交于P1,∠EAP1与∠FBP1的平分线交于P2 ;依此类推,则∠P5=______.(用α、β表示)



-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是黄金分割比(黄金分割比0.618)著名的“断臂维纳斯”便是如此.此外最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是黄金分割比.若某人满足上述两个黄金分割比例,且腿长为103cm,头顶至脖子下端的长度为25cm,则其身高可能是( )

A.165cmB.170cmC.175cmD.180cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数yx3的图象与反比例函数y
 (k为常数,且k0)的图象交于A(1,a),B两点.
(k为常数,且k0)的图象交于A(1,a),B两点.(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,点A、B为函数L图象上的任意两点,点A坐标为(x1,y1),点B坐标为(x2,y2),把式子
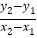 称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1=
称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1= 时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=
时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=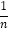 (n为正整数)时,函数K从x1到x2的平均变化率是_____.
(n为正整数)时,函数K从x1到x2的平均变化率是_____.
相关试题

