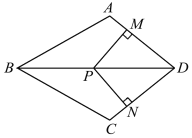
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
参考答案:
【答案】证明见解析.
【解析】
试题分析:(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;
(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.
试题解析:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
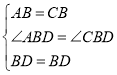 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)如图,已知抛物线
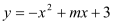 与
与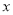 轴交于A,B两点,与
轴交于A,B两点,与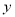 轴交于点C,点B的坐标为(3,0)。
轴交于点C,点B的坐标为(3,0)。(1)求m的值及抛物线的顶点坐标;
(2)点P是抛物线对称轴
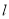 上的一个动点,当PA+PC的值最小时,求点P的坐标。
上的一个动点,当PA+PC的值最小时,求点P的坐标。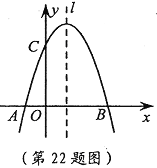
-
科目: 来源: 题型:
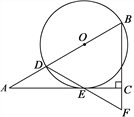
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
(1)求证:△BDF是等边三角形;
(2)连接AF、DC,若BC=3,写出求四边形AFCD面积的思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P在第二象限,若该点到x轴的距离为3,到y轴的距离为1,则点P的坐标是( )
A.(﹣1,3)
B.(﹣3,1)
C.(3,﹣1)
D.(1,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=ax2的图象过点(1,﹣2),则a的值是_____,在对称轴左侧,y随x的增大而_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A的坐标为(0,m),且m≠0,点B的坐标为(n,0),将线段AB绕点B旋转90°,分别得到线段B P1,B P2,称点P1,P2为点A关于点B的“伴随点”,图1为点A关于点B的“伴随点”的示意图.
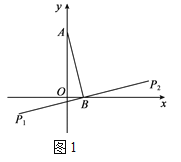
(1)已知点A(0,4),
①当点B的坐标分别为(1,0),(-2,0)时,点A关于点B的“伴随点”的坐标分别为 ;
②点(x,y)是点A关于点B的“伴随点”,直接写出y与x之间的关系式;
(2)如图2,点C的坐标为(-3,0),以C为圆心,
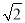 为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.
为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.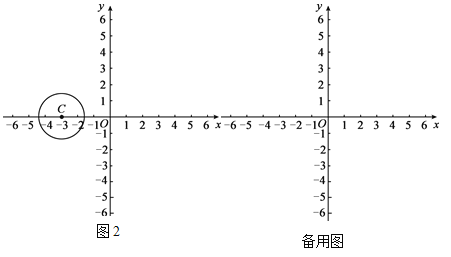
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B坐标分别为A(0,a),B(b,a),且实数a,b满足(a﹣3)2+|b﹣5|=0,现同时将点A,B分别向下平移3个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
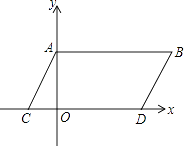
(1)求点C,D的坐标及四边形ABDC的面积;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=S四边形ABDC?若存在这样一点,求出点M的坐标;若不存在,试说明理由.
相关试题

