【题目】在平面直角坐标系xOy中,点A的坐标为(0,m),且m≠0,点B的坐标为(n,0),将线段AB绕点B旋转90°,分别得到线段B P1,B P2,称点P1,P2为点A关于点B的“伴随点”,图1为点A关于点B的“伴随点”的示意图.
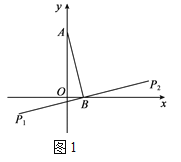
(1)已知点A(0,4),
①当点B的坐标分别为(1,0),(-2,0)时,点A关于点B的“伴随点”的坐标分别为 ;
②点(x,y)是点A关于点B的“伴随点”,直接写出y与x之间的关系式;
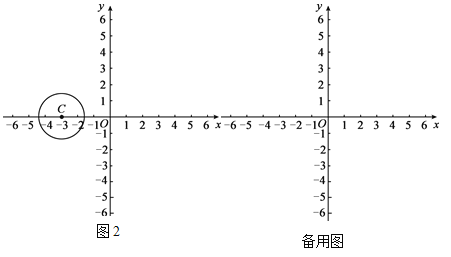
(2)如图2,点C的坐标为(-3,0),以C为圆心, ![]() 为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.
为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.
参考答案:
【答案】(1)①(-3,-1),(5,1);(-6,2),(2,-2);②y=x-4或y=-x-4.
(2)-5≤m≤-1或1≤m≤5
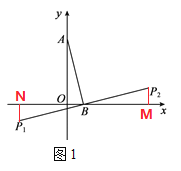
【解析】试题分析:(1)①作![]() ⊥x轴于点M,作
⊥x轴于点M,作![]() ⊥x轴于点N,根据已知条件易证
⊥x轴于点N,根据已知条件易证![]() ≌
≌![]() ≌
≌![]() ,根据全等三角形的性质可得
,根据全等三角形的性质可得![]() =OB=
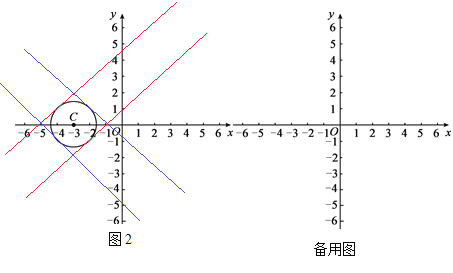
=OB= ![]() ,OA=BM=BN,根据A(0,4),当点B的坐标为(1,0)时,即可求得点A关于点B的“伴随点”的坐标分别为(-3,-1),(5,1);根据A(0,4),当点B的坐标为(-2,0)时,即可求得点A关于点B的“伴随点”的坐标分别为(-6,2),(2,-2);②由①可知,x=y+4或-x-y=4,即可得y与x之间的关系式为y=x-4或y=-x-4;(2)设点A的坐标为(0,m),点(x,y)是点A关于点B的“伴随点”,由(1)的方法可得y=x-m或y=-x-m,当直线y=x-m相切时,如图(图中的红线),根据直线y=x-m与x轴、y轴所围成的三角形为等腰直角三角形、切线的性质。勾股定理可求得m=1,或m=5,即可得1≤m≤5,当直线y=-x-m相切时,如图(图中的蓝线),同理可得-5≤m≤-1,所以点A的纵坐标m的取值范围为-5≤m≤-1或1≤m≤5.
,OA=BM=BN,根据A(0,4),当点B的坐标为(1,0)时,即可求得点A关于点B的“伴随点”的坐标分别为(-3,-1),(5,1);根据A(0,4),当点B的坐标为(-2,0)时,即可求得点A关于点B的“伴随点”的坐标分别为(-6,2),(2,-2);②由①可知,x=y+4或-x-y=4,即可得y与x之间的关系式为y=x-4或y=-x-4;(2)设点A的坐标为(0,m),点(x,y)是点A关于点B的“伴随点”,由(1)的方法可得y=x-m或y=-x-m,当直线y=x-m相切时,如图(图中的红线),根据直线y=x-m与x轴、y轴所围成的三角形为等腰直角三角形、切线的性质。勾股定理可求得m=1,或m=5,即可得1≤m≤5,当直线y=-x-m相切时,如图(图中的蓝线),同理可得-5≤m≤-1,所以点A的纵坐标m的取值范围为-5≤m≤-1或1≤m≤5.
试题解析:
(1)①(-3,-1),(5,1);(-6,2),(2,-2).
②y=x-4或y=-x-4.
(2)-5≤m≤-1或1≤m≤5
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P在第二象限,若该点到x轴的距离为3,到y轴的距离为1,则点P的坐标是( )
A.(﹣1,3)
B.(﹣3,1)
C.(3,﹣1)
D.(1,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
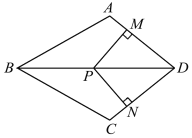
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=ax2的图象过点(1,﹣2),则a的值是_____,在对称轴左侧,y随x的增大而_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B坐标分别为A(0,a),B(b,a),且实数a,b满足(a﹣3)2+|b﹣5|=0,现同时将点A,B分别向下平移3个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
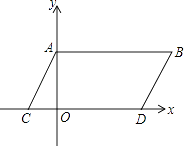
(1)求点C,D的坐标及四边形ABDC的面积;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=S四边形ABDC?若存在这样一点,求出点M的坐标;若不存在,试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若2×4m×8m=231,则m的值为( )
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知tanβ=22.3,则β=(精确到1″)
相关试题

