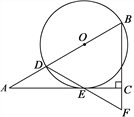
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
(1)求证:△BDF是等边三角形;
(2)连接AF、DC,若BC=3,写出求四边形AFCD面积的思路.
参考答案:
【答案】(1)证明见解析;(2)思路见解析.
【解析】试题分析:(1)连接OE,因AC切⊙O于点E,根据切线的性质可得∠OEA=90° ;再由∠A=30°,∠ACB=90°,根据三角形的内角和定理可得∠AOE=60°,∠B=60°因OD=OE,可得∠ODE=∠OED=60°,所以∠F=∠B=∠ODE,即可判断△BDF是等边三角形 ;(2)如图,作DH⊥AC于点H,求四边形AFCD的面积思路有以下几步:①由∠ACB=90°,∠BAC=30°,BC=3,可求AB,AC的长;②由∠AEO=90°,∠OAE=30°,可知AO=2OE,可求AD,DB,DH的长; ③由(1)可知BF=BD,可求CF的长; ④由AC,DH,CF的长可求四边形AFCD的面积.
试题解析:
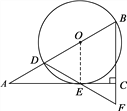
(1)证明:连接OE.
∵AC切⊙O于点E,
∴![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴△BDF是等边三角形.
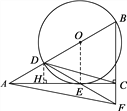
(2)如图,作DH⊥AC于点H.
①由∠ACB=90°,∠BAC=30°,BC=3,可求AB,AC的长;
②由∠AEO=90°,∠OAE=30°,可知AO=2OE,可求AD,DB,DH的长;
③由(1)可知BF=BD,可求CF的长;
④由AC,DH,CF的长可求四边形AFCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店老板去图书批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书数量比第一次多10本.当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式由左边至右边的变形中,属于因式分解的是( )
A. x2+5x﹣1=x(x+5)﹣1 B. x2﹣4+3x=(x+2)(x﹣2)+3x
C. x2﹣9=(x+3)(x﹣3) D. (x+2)(x﹣2)=x2﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)如图,已知抛物线
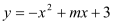 与
与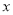 轴交于A,B两点,与
轴交于A,B两点,与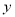 轴交于点C,点B的坐标为(3,0)。
轴交于点C,点B的坐标为(3,0)。(1)求m的值及抛物线的顶点坐标;
(2)点P是抛物线对称轴
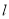 上的一个动点,当PA+PC的值最小时,求点P的坐标。
上的一个动点,当PA+PC的值最小时,求点P的坐标。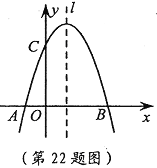
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P在第二象限,若该点到x轴的距离为3,到y轴的距离为1,则点P的坐标是( )
A.(﹣1,3)
B.(﹣3,1)
C.(3,﹣1)
D.(1,3) -
科目: 来源: 题型:
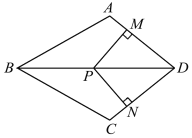
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=ax2的图象过点(1,﹣2),则a的值是_____,在对称轴左侧,y随x的增大而_____.
相关试题

