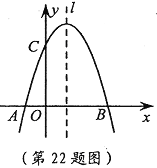
【题目】(本题10分)如图,已知抛物线![]() 与
与![]() 轴交于A,B两点,与
轴交于A,B两点,与![]() 轴交于点C,点B的坐标为(3,0)。
轴交于点C,点B的坐标为(3,0)。
(1)求m的值及抛物线的顶点坐标;
(2)点P是抛物线对称轴![]() 上的一个动点,当PA+PC的值最小时,求点P的坐标。
上的一个动点,当PA+PC的值最小时,求点P的坐标。
参考答案:
【答案】(1)m=2,(1,4);(2)(1,2).
【解析】
试题分析:(1)把点B的坐标为(3,0)代入![]() ,解方程即可得m的值,求出m的值后把抛物线化为顶点式即可得抛物线的顶点坐标;(2)连接BC交抛物线的对称轴于点P,此时PA+PC的值最小,利用待定系数法求得直线BC的解析式,再求点P的坐标即可.
,解方程即可得m的值,求出m的值后把抛物线化为顶点式即可得抛物线的顶点坐标;(2)连接BC交抛物线的对称轴于点P,此时PA+PC的值最小,利用待定系数法求得直线BC的解析式,再求点P的坐标即可.
试题解析:(1)把点B的坐标为(3,0)代入得:![]() ,
,
解得m=2,
∴![]()
∵![]()
∴顶点坐标为(1,4).
(2)连接BC交抛物线的对称轴l于点P,此时PA+PC的值最小,
设Q是直线l上任意一点,连结AQ,CQ,BQ,
∵直线L垂直平分AB,
∴AQ=BQ,AP=BP,
∴AQ+CQ=BQ+CQ≥BC,
BC=BP+CP=AP+CP,
即AQ+CQ≥AP+CP
设直线BC的解析式为y=kx+b(k≠0),
把(3,0),(0,3)代入得,
![]() ,解得
,解得![]() ,
,
∴直线BC的解析式为y=-x+3,
当x=1时,y=-1+3=2.
答:当PA+PC的值最小时,点P的坐标为(1,2).

-
科目: 来源: 题型:
查看答案和解析>>【题目】用计算器求tan35°的值,按键顺序是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店老板去图书批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书数量比第一次多10本.当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式由左边至右边的变形中,属于因式分解的是( )
A. x2+5x﹣1=x(x+5)﹣1 B. x2﹣4+3x=(x+2)(x﹣2)+3x
C. x2﹣9=(x+3)(x﹣3) D. (x+2)(x﹣2)=x2﹣4
-
科目: 来源: 题型:
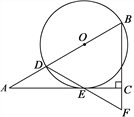
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
(1)求证:△BDF是等边三角形;
(2)连接AF、DC,若BC=3,写出求四边形AFCD面积的思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P在第二象限,若该点到x轴的距离为3,到y轴的距离为1,则点P的坐标是( )
A.(﹣1,3)
B.(﹣3,1)
C.(3,﹣1)
D.(1,3) -
科目: 来源: 题型:
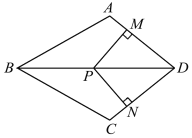
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
相关试题

