【题目】如图,在平面直角坐标系中,点A,B坐标分别为A(0,a),B(b,a),且实数a,b满足(a﹣3)2+|b﹣5|=0,现同时将点A,B分别向下平移3个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB. 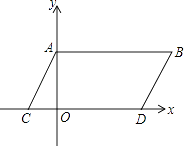
(1)求点C,D的坐标及四边形ABDC的面积;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=S四边形ABDC?若存在这样一点,求出点M的坐标;若不存在,试说明理由.
参考答案:
【答案】
(1)解:∵(a﹣3)2+|b﹣5|=0,
∴a=3,b=5,
∴点A(0,3),B(5,3).
将点A,B分别向下平移3个单位,再向左平移1个单位,得到点C、D,
∴点C(﹣1,0),D(4,0).
由AB平移得出CD可知,AB∥CD,且AB=CD=5,
∴四边形ABDC为平行四边形,
∴S四边形ABDC=5×3=15.
(2)解:设存在点M(0,y),
根据题意得:S△MCD= ![]() ×5|y|=S四边形ABDC=15,
×5|y|=S四边形ABDC=15,
∴ ![]() ×5|y|=15,解得:y=±6,
×5|y|=15,解得:y=±6,
∴存在点M(0,6)或(0,﹣6),使S△MCD=S四边形ABDC.
【解析】(1)由偶次方及绝对值的非负性可求出a、b的值,进而即可得出点A、B的坐标,再根据平移的性质可得出点C、D的坐标以及四边形ABDC为平行四边形,套用平行四边形的面积公式即可求出四边形ABDC的面积;(2)设存在点M(0,y),根据三角形的面积结合S△MCD=S四边形ABDC , 即可得出关于y的含绝对值符号的一元一次方程,解之即可得出结论.
【考点精析】本题主要考查了三角形的面积的相关知识点,需要掌握三角形的面积=1/2×底×高才能正确解答此题.
-
科目: 来源: 题型:
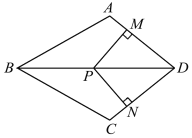
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=ax2的图象过点(1,﹣2),则a的值是_____,在对称轴左侧,y随x的增大而_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A的坐标为(0,m),且m≠0,点B的坐标为(n,0),将线段AB绕点B旋转90°,分别得到线段B P1,B P2,称点P1,P2为点A关于点B的“伴随点”,图1为点A关于点B的“伴随点”的示意图.
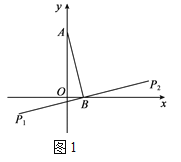
(1)已知点A(0,4),
①当点B的坐标分别为(1,0),(-2,0)时,点A关于点B的“伴随点”的坐标分别为 ;
②点(x,y)是点A关于点B的“伴随点”,直接写出y与x之间的关系式;
(2)如图2,点C的坐标为(-3,0),以C为圆心,
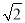 为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.
为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.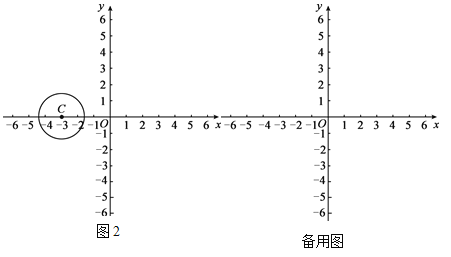
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2×4m×8m=231,则m的值为( )
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知tanβ=22.3,则β=(精确到1″)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形OEFG中,点A和点F的坐标分别为 (3,2),(-1,-1),则两个正方形的位似中心的坐标是( )

A.(1,0)
B.(-5,-1)
C.(1,0)或(-5,-1)
D.(1,0)或(-5,-2)
相关试题

