【题目】计算题
(1)计算:|﹣4|﹣(﹣2)2+ ![]() ﹣(
﹣( ![]() )0
)0
(2)解不等式组  .
.
参考答案:
【答案】
(1)解:原式=4﹣4+3﹣1=2;
(2)解: 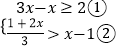
解不等式①得,x≥1,
解不等式②得,x<4,
所以不等式组的解集是1≤x<4.
【解析】(1)本题主要考查了实数的运算法则,根据绝对值、零指数幂、平方根等运算法则进行计算即可得到答案.
(2)根据一元一次不等式组的解法,先得到解个一元一次不等式的值,再得到不等式组的解集即可.
【考点精析】本题主要考查了零指数幂法则和一元一次不等式组的解法的相关知识点,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产
 、
、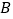 两种产品共50件.已知生产一件
两种产品共50件.已知生产一件 种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件
种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件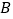 种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.
种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.(1)设生产
 种产品
种产品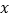 件,完成表格:
件,完成表格: 产品
产品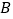 产品
产品生产数量(件
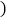
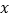 件
件件
需甲种原料(千克)
需乙种原料(千克)
(2)按要求安排
 、
、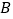 两种产品的件数有几种方案?请你设计出来.
两种产品的件数有几种方案?请你设计出来.(3)以上方案哪种利润最大?是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】欧城物业为美化小区,要对面积为9600平方米的区域进行绿化,计划安排甲、乙两个园林队完成,已知甲园林队每天绿化面积是乙园林队每天绿化面积的2倍,并且甲、乙两园林队独立完成面积为800平方米区域的绿化时,甲园林队比乙园林队少用2天.
(1)求甲、乙两园林队每天能完成绿化的面积分别是多少平方米.
(2)物业每天需付给甲园林队的绿化费用为0.4万元,乙园林队的绿化费用为0.25万元,如果这次绿化总费用不超过10万元,那么欧城物业至少应安排甲园林队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y=
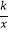 (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 .
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 . 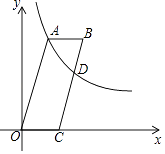
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )

A. ∠1=∠3 B. ∠B+∠BCD=180°
C. ∠2=∠4 D. ∠D+∠BAD=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如何求tan75°的值?按下列方法作图可解决问题.如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BM上截取线段BD,使BD=AB,连接AD.连接此图可求得tan75°的值为( )

A.2-
B.2+
C.1+
D.
-1 -
科目: 来源: 题型:
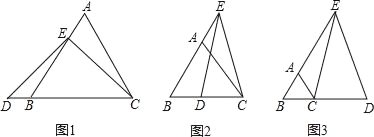
查看答案和解析>>【题目】已知△ABC为等边三角形,E为射线BA上一点,D为直线BC上一点,ED=EC.
(1)当点E在AB的上,点D在CB的延长线上时(如图1),求证:AE+AC=CD;
(2)当点E在BA的延长线上,点D在BC上时(如图2),猜想AE、AC和CD的数量关系,并证明你的猜想;
(3)当点E在BA的延长线上,点D在BC的延长线上时(如图3),请直接写出AE、AC和CD的数量关系.
相关试题

